Is the area of a line really $0$?

Question

Let's take a square with side $A$. The area of this is defined as $A\times A$. The way I explained this to myself is by reapeatedly deviding the square till I reached a single line. Then stacking up lines one on top of the other $A$ times.

But if the area of a line was really $0$ no matter how many lines were stacked up, they would always have an area of $0$.(would exist in one dimension only)

Another way to see this is defining a function $V(F)$ which gives the volume of two dimensional figure $F$. If this volume became $0$ , no matter how many such Figures I stack up on each other they would never have a volume.

When this is combined with physics it makes a little more sense. Even if I were to chop up a cube infinitely I could never reduce its height to less than the Planck length. This means that the volume would be $Area \times ℓP$ (Planck length)

So the question is for a three dimensional object to exist must every two dimensional object have a non zero volume?

Answer 1

You've touched on one of the reasons why a careful axiomatization of measure theory is important. How you answer your question depends on how you are defining your notion of "volume"/"area" (what we generally call "measure").

• Let's say in your setup you give line segments of length $1$ a nonzero volume $c$. And let's suppose that your notion of volume is additive (in the sense that the volume of the union of disjoint regions is equal to the sum of the volumes of the individual regions). One might think of a $1 \times 1$ square as stacking infinitely many (actually, an uncountable infinitude of) copies of this line segment. Then your $1 \times 1$ square would have infinite volume since each segment has volume $c$ and you are combining infinitely many of these segments.
• On the other hand, if we say that these line segments have zero volume, then this seems to suggest that the $1 \times 1$ square has zero volume as well, since it is made up of infinitely many segments each having zero volume.
• The "solution" to this paradox that is established in measure theory is to restrict the additivity property to only countable unions. That is, if $E_1, E_2,\ldots$ are a countable collection of disjoint sets, then $\text{volume}\left(\bigcup_{i =1}^\infty E_i \right) = \sum_{i=1}^\infty \text{volume}(E_i)$; we do not require that this property holds for uncountable collections of disjoint sets. Then, in the case of Lebesgue measure in two-dimensional space, we assign "two-dimensional" regions volume in the usual sense ("area"), and we assign "one-dimensional" regions (like line segments) zero volume. The "paradox" in the previous bullet-point does not occur simply because we do not require our notion of volume to be additive across uncountable collections of disjoint sets (like stacking uncountably many line segments to make a square). This is just a description of Lebesgue measure, however; you can assign measures in other non-intuitive ways.

Answer 2

As shown in this answer, for any sum of non-negative numbers to make sense, only countably many terms can be non-zero. So if we chop up the unit square into lines, each one indexed by the real number which is its $y$-coordinate, we cannot expect the sum of the uncountably many $0$ areas to give a meaningful result.

There is a similar problem when trying to assign a uniform probability measure on the integers. To divide the total measure of $1$ among the infinitely many integers, we need to assign a measure of $0$ for each integer. However, summing the countably many zeros, we get $0$. So we cannot have a uniform probability measure on the integers.

This indicates that we cannot divide up a square into uncountably many lines of $0$ area and add those areas to get the area of the square.

Answer 3

Your interpretation of the area of the square makes sense if each of your "lines" has a width of $1$ (that is why you have exactly $A$ such lines). Usual lines have zero width and you need to have uncountably infinitely many of them to obtain a height of $A$.

Answer 4

The answer to your question is no.

You have the right idea that decomposing areas into arealess constituents provides no help in finding areas. Of course, no one does that. One finds a reference area and uses that to measure other areas. For instance, one declares a particular figure (commonly a square or rectangle) to have area $1$. Then other areas are determined to be multiples of that area. In short, you divided too far if you divided all the way down to lines.

The same thing can be done for volumes: declare a unit volume and measure other volumes in terms of that volume.

If you read the old Greek geometers they a constantly measuring with respect to some other figure, for instance, this line segment is twice as long as that line segment. They let the initial geometry dictate the scale of the magnitudes.

You may wonder how we can deal with areas and volumes that are not unions of unit squares and unit volumes. The underlying method is to proceed iteratively through dimensions. Start by declaring a unit length. Then, declare that a rectangle of side lengths $m$ and $n$ has area $mn$. Then declare that a rectangular parallelpiped of side lengths $m$, $n$, and $p$ has volume $mnp$. So now we have reference volumes of any size.

Decompose a region containing a figure into rectangles. If there are any rectangles in the region that do not meet the figure, just delete those from the region and continue with this reduced region. The area of the region is the sum of the areas of the rectangles and is an upper bound for the area of the figure. A lower bound on the area of the figure is the sum of the areas of the rectangles contained in the figure. Call the lower bound $m$ and the upper bound $M$. We know that the area of the figure is in the interval $[m,M]$. Suppose the longest edge of any rectangle is $L$. Now make a new rectangulation where the length of the longest edge is $\leq L$. We expect this finer partition to have more rectangles which we discard, so the upper bound decreases, and to include additional area interior to the figure, so the lower bound increases. If the lower bound and upper bound approach the same value, $a$, in the limit as the longest edge goes to zero (for every sequence of refining rectangulations), then the area of the figure is $a$. If the two limits do not approach the same value or the value depends on details of the rectangulation, then the area does not exist.

Notice that this method does partition the figure into pieces and we sum up the contributions of these pieces, but we never actually have pieces of zero area. We contemplate what would happen in the limit of having all pieces have zero area, but we never actually work with such pieces.

An analogous process, partitioning to produce an inner volume (lower bound) and outer volume (upper bound) is used for volumes (and this process can be continued to higher dimensions). Again, if the two bounds approach the same constant as the length of the longest edge goes to zero for any sequence of decompositions into rectangular parallelpipeds, that constant is the volume.

(This diagram (by Blacklemon67 at the English Wikipedia, used unmodified under CC-BY-SA 3.0) 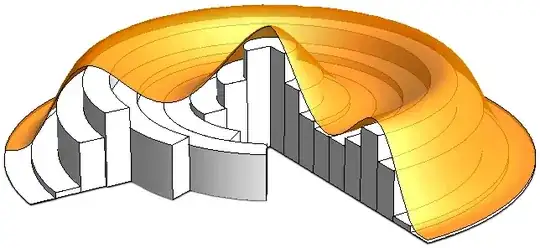shows a variant of this method using the analogue of rectangular parallelpipeds in circular polar coordinates to produce an inner volume. Finer partitioning in the radial direction will allow the circular cylindrical shells to more closely follow the contour of the surface bounding the volume and hence increase toward the desired volume.)

So what happens to a line (segment)? This is a figure in the plane, so we can ask for its area. For any enclosing region, we get some finite outer area, but there are no rectangles contained in the line, so we always get zero inner area. As we refine and refine the rectangulation, we gradually discard the area outside the line. In the limit, we would discard all the area outside the line, and the two bounds for the area converge to zero. So the area of a line (segment) is zero.

So what causes the jump between "this collection of line segments has zero area because each line segment has zero area" and "this figure has positive area even though we can imagine decomposing it into zero area parts"? Fundamentally, this depends on what the word "area" means. We don't define an area based on the number of line segments a figure can be decomposed into. Line segments are too small (in area) to support any nonzero notion of area. We choose (not just in this Answer) to define area in terms of rectangles. Decomposition into rectangles (however many and however large or small) is a process that can arrive at an area. Decomposition into line segments immediately leaves the arena of things with areas so immediately cuts off access to the notion of area.

One might object that one should always be able to decompose into line segments and should get a sensible notion of area when doing so. But this doesn't always happen. Consider the function $f(x) = \frac{x}{x}$. We might (incorrectly) simplify this to $1$. However, $f$ is defined by the expression we gave and that expression is undefined when $x = 0$. As a consequence, $f$ has no value when $x = 0$. $f$ has a sensible value, $1$, all the way down to $x = 0$, but is not sensible at $x = 0$. A similar phenomenon occurs with area : we get sensible areas (bounds) by dividing into rectangles with bounded longest side length as that bound decreases all the way down to zero, but we do not get a sensible result when the bound on the length of the longest side is set to zero.

This can be generalized. One takes some properties of areas (and analogues in higher dimensions) and calls anything which satisfies these properties a "measure": areas are nonnegative. The empty figure contains no area. A finite or countably infinite collection of disjoint figures have collective area equal to the sum of their individual areas. (Note that an infinite collection of areas need not have a finite combined area, so we should be careful about summing up infinitely many areas.) One then can define an inner measure (our lower bounds, above) and an outer measure (our upper bounds, above) and then use the same approach as above to determine whether a figure has an area and if so, what it is.