0

enter image description here

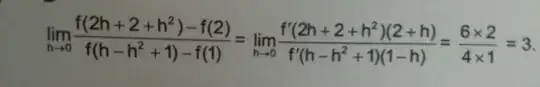
This was the problem. And they solved it by doing this: enter image description here

I don't understand what they they did. Can someone help me understand it?

Dhruv Agarwal
  • 73
  • 5
    They attempted to use L'Hopital's rule, but they did it incorrectly. The chain rule tells us that the derivative of the numerator is $f'(2h+2+h^2)\times (2+2h)$ and, similarly, the demoniator yields $f'(h-h^2-1)\times (1-2h)$ These errors do not change the final answer. – lulu Nov 29 '20 at 12:24
  • @lulu I agree, but as pointed out in an answer, another mistake in this approach is the assumption that limits of $f'(x)$ exist as $x$ goes to $1$ or to $2$. – David K Nov 29 '20 at 16:26
  • @DavidK $f'(1)$ and $f'(2)$ are given, so I think it's fair to assume that $f(x)$ is differentiable at least near $1$ and $2$. – lulu Nov 29 '20 at 16:34
  • @lulu It is possible for a function to be differentiable at a point but not in any neighborhood of that point: https://math.stackexchange.com/q/108388/139123. The usual examples have only one differentiable point, but it's easy enough to set up two such points. – David K Nov 29 '20 at 16:45

2 Answers2

1

This is some version of the "l'Hospital" rule. Or some truncated version of Taylor expansion. I don't like it.

What you can do is this : using Taylor expansion for function $f$ at point $x$, you have : $$f(y)=f(x)+(y-x)f'(x) + o(y-x)$$ So, putting $x=2$ and $y=2+2h+h^2$ : $$f(2h+2+h^2) = f(2) + (2h+h^2)f'(2)+o(h) = f(2)+h((2+h)f'(2)+o(1))$$ and with $x=1$ and $y=1+h-h^2$ : $$f(1+h-h^2)=f(1)+(h-h^2)f'(1)+o(h) = f(1)+h((1-h)f'(1)+o(1))$$ so $$\frac{f(2h+2+h^2)-f(2)}{f(1+h-h^2)-f(1)} = \frac{h((2+h)f'(2)+o(1))}{h((1-h)f'(1)+o(1))} = \frac{(2+h)f'(2)+o(1)}{(1-h)f'(1)+o(1)}$$ If, and ONLY IF, $f'(1)\ne0$, then this fraction has limit $\frac{2f'(2)}{f'(1)}$.

The solution provided is not false, but the first equality needs a lot of justifications, so I don't like it. But maybe there's a theorem used in american teaching (l'Hospital ?) that we don't use in France, that could justify the solution.

Nicolas FRANCOIS
  • 4,846
1

The given solution is not correct - although its final result is right - because we do not know whether $f'$ exists around $2$ and $1$, resp.

So, we should only use the existence of the two given derivatives and this is possible:

We know

$$\lim_{t\to 0}\frac{f(2+t)-f(2)}{t}=f'(2)=6 \text{ and } \lim_{t\to 0}\frac{f(1+t)-f(1)}{t}=f'(1)=4$$

Hence, only using this, rewrite \begin{eqnarray*}\frac{f(2+2h+h^2)-f(2)}{f(1+h-h^2)-f(1)} & = & \frac{f(2+2h+h^2)-f(2)}{2h+h^2}\cdot\frac{h-h^2}{f(1+h-h^2)-f(1)}\cdot\frac{2h+h^2}{h-h^2}\\ & \stackrel{h\to 0}{\longrightarrow} & f'(2)\cdot \frac 1{f'(1)}\cdot 2 = 3 \end{eqnarray*}

trancelocation
  • 32,243