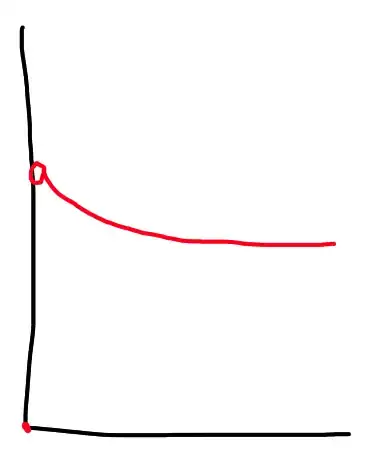
I recently came across the following example of a function which is discontinuous at a point:
The cost of a sushi buffet is calculated by weighing your plate, where you are then charged £10 per pound. As part of a promotion, if you manage to fill your plate so that the weight is precisely 1lbs, you get your meal for free.
This is a nice way to motivate a function like $$f(x) = \begin{cases}10\,x\hfil&\text{$x\neq 1$}\\\hfil0\hfil&\text{$x=1$}\end{cases}$$ which are nice for illustrating the idea of a limit to students.
Are there any other real-world examples of functions like this, for the sake of explaining limits? Ideally one where you would actually want the limiting value, and not the assigned value, to motivate the concept further. (Apart from the obvious difference quotient.)