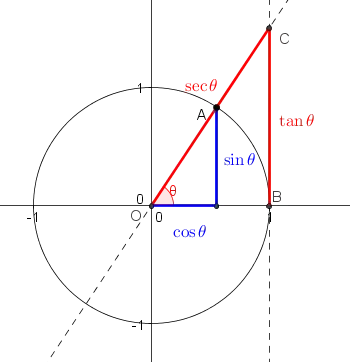
I read that $ 0 < \cos(\theta) < \dfrac{\sin(\theta)}{\theta} < \dfrac{1}{\cos(\theta)}$ for $\theta \in (0,\dfrac{\pi}{2})$. I am confused about the middle part. I don't find it intutive (even from the graph). Please explain me why this is so.
Asked
Active
Viewed 56 times
0
-
1Are you familiar with elementary differential calculus? If so, you could apply the Mean Value Theorem to the functions $\mathrm{tg}x-x$ respectively $x-\sin x$, with $x \in \left(0, \frac{\pi}{2}\right)$ and take a look at the signs of the derivatives of these functions. If on the other hand you are not yet familiar with differential calculus, there is no rigorous way to accede to a proof. – ΑΘΩ Nov 26 '20 at 09:45
-
2Here is one way. – David Mitra Nov 26 '20 at 09:48
-
@DavidMitra Alas all the answers on the referenced page -- although they are indeed worthy for their intuitive power of explaining why these inequalities hold in the first place -- do not constitute rigorous proofs. – ΑΘΩ Nov 26 '20 at 09:50
-
1@ΑΘΩ: the OP does not seem to be after a proof. – Nov 26 '20 at 09:51
-
@YvesDaoust Quite true. I just wanted to point things out clearly. – ΑΘΩ Nov 26 '20 at 09:52
-
2Does this answer your question? How do I get $\cos{\theta} \lt \frac{\sin{\theta}}{\theta} \lt 1$? Found using Approach0. – Toby Mak Nov 26 '20 at 10:09
3 Answers
3
Hint : For $0 < \theta < \frac{\pi}{2}$, $$\cos(\theta) < \frac{\sin(\theta)}{\theta} \Longleftrightarrow \theta < \tan(\theta)$$
TheSilverDoe
- 29,720
1
On the picture, it seems obvious that the sine is shorter than the arc $AB$, and if you wind the tangent on the circle, you end up past $A$. A stronger argument is that the area of the triangle $OBC$ exceeds that of the sector $OBA$.
Hence
$$\frac\sin\theta<\theta$$ and $$\theta<\tan\theta.$$
0
$f(x)=x\cos x-\sin x \implies f'(x)=\cos x-x\sin x-\cos x <0, \in (0,\pi/2).$So $f(x)$ is a decreasing function. Then $x>0 \implies f(x) <f(0)=0 \implies x \cos x-\sin x<0 \implies \cos x<\frac{\sin x}{x}, x\in (0,\pi/2).$
Z Ahmed
- 43,235
-
@Z Ahmed Only $f$ is a function, not $f(x)$. $f(x)$ is a value that the function $f$ takes in a specific argument. – ΑΘΩ Nov 26 '20 at 09:51
-
Don't you need the result you are trying to prove in order to take the derivatives of $\sin$ and $\cos$? – David Mitra Nov 26 '20 at 09:54
-
@DavidMitra Not necessarily, if he considers the trigonometric functions being introduced the right and proper way, namely as the real and imaginary parts of the complex exponential $\mathbb{R} \ni x \mapsto \mathrm{e}^{\mathrm{i}x} \in \mathbb{C}$. – ΑΘΩ Nov 26 '20 at 09:56
-
-
@David Mitra Upon introducing the trigonometric functions rigorously -- as mentioned in my comment above -- one immediately obtains the power series for each of the two main trigonometric functions. This is what enables one to show right away that $\displaystyle\lim_{z \to 0}\frac{\sin z}{z}=1$ and to thus deduce the differential relations between $\sin$ and $\cos$, based on the additivity relations between them. In an even more straightforward way, the derivatives can be right away evaluated from the definitions involving the complex exponential (whose derivative is immediate to establish). – ΑΘΩ Nov 28 '20 at 01:45