I have a problem with exercises with sequences given by recursion when I need to "prove convergence and find limit if it exists" and I am given a recursion of that kind:
$$ x_{1+n} = \frac{1}{2 + x_{n}}, x_1 \in (0 ; \infty)$$
It is fairly easy to find the limit - I just assume that the limit exists in $ \mathbb{R}$ and then use arithmetic properties of limits: $$\lim_{n \to \infty} x_{n+1} = \lim_{n \to \infty} x_{n}$$ $$\lim_{n \to \infty} x_{n} = l, l \in \mathbb{R}>0$$
Taking my recursion: $$l = \frac{1}{2 + l}$$ $$l^2 +2l - 1 = 0$$ $$l_1 = \sqrt{2} - 1 \in D$$ $$l_2 = -1 - \sqrt{2} \notin D$$
So my only possible limit in $ \mathbb{R}$ is $l = \sqrt{2} - 1$. That is if I can actualy prove that the limit exists - that is: the sequence is monotonous and bounded. And here is my problem - it is just impossible to analyse without computer the difference of:
$$x_{1+n} - x_{n} = \frac{1}{2 + x_{n}} - x_{n}$$
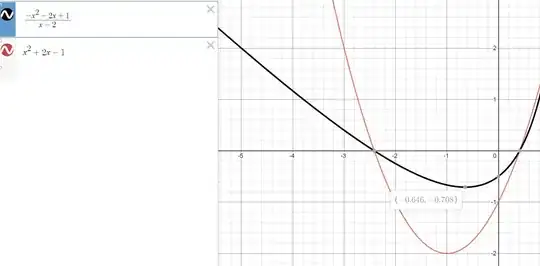
In search of limits I just multiply both sides of equation by $ \lim_{n \to \infty} x_{n} = l$ and it is impossible to do so here, so I get: $$x_{1+n} - x_{n} = \frac{-x_{n}^2-2x_n+1}{2 + x_{n}}$$
Then I can't tell when it is bigger than $0$ to analyse monotonicity and I can't the see for which values o $n$ which values of $n+1$ i get (to get the boundary) because min value gets crazy.
So I just waneted to ask - am I missing something? Is it possible to make here $x_{1+n} - x_{n} = \frac{-x_{n}^2-2x_n+1}{2 + x_{n}}$ an equality with $0$ and analyse simpler function (red one on the picture)?