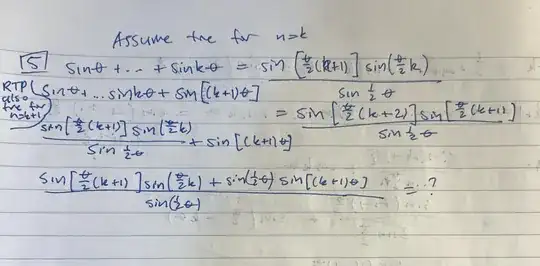1

Prove that $$\sin\theta+\sin2\theta+\sin3\theta+\cdots+\sin n\theta=\frac{\sin\frac{(n+1)\theta}2\sin\frac{n\theta}2}{\sin\frac\theta2},n\ge1,n\in\mathbb Z.$$

I have solved the base case $n = 1$ and prepared the assumption $n = k$. After I substitute the assumption into the induction step at $n = k+1$ I get lost, as I don't know how to successfully manipulate the numerator into the RHS. Any hints?

Parcly Taxel
  • 103,344
user71207
  • 1,543
  • I'm sure this question has been asked & answered on this website before. – Gerry Myerson Nov 21 '20 at 05:38
  • 1
    Compare https://math.stackexchange.com/questions/1267244/sum-of-series-sin-theta-sin-2-theta-sin-3-theta-dots and https://math.stackexchange.com/questions/297452/sines-and-cosines-of-angles-in-arithmetic-progression and https://math.stackexchange.com/questions/17966/how-can-we-sum-up-sin-and-cos-series-when-the-angles-are-in-arithmetic-pro and https://math.stackexchange.com/questions/831159/evaluating-sum-n-199-sinn and https://math.stackexchange.com/questions/1349466/calculating-sum-k-0n-sink-theta and probably many, many others. – Gerry Myerson Nov 21 '20 at 05:41
  • Yeah thank you I was looking for it too but I couldn't find an already asked version – user71207 Nov 21 '20 at 05:44
  • 1
    Does this answer your question? Calculating $\sum_{k=0}^{n}\sin(k\theta)$ – John Omielan Nov 21 '20 at 06:18
  • I dont really understand these answers since I haven't done complex numbers yet. Ive posted what I have tried so far as an answer: would you be able to have a look? – user71207 Nov 21 '20 at 07:27
  • I dont really understand these answers since I haven't done complex numbers yet. Ive posted what I have tried so far as an answer: would you be able to have a look? – user71207 Nov 21 '20 at 07:27

2 Answers2

1

enter image description here

Here is what I have done so far. I cant think of a way to manipulate the LHS into the RHS

user71207
  • 1,543
0

BIG HINT

(Warning: I've written the entire inductive step, just cryptically)

$$\sin{0.5(n+2)}\theta\sin{0.5(n+1)\theta}-\sin{0.5(n+1)}\theta\sin{0.5n\theta}$$

$$=\sin{0.5(n+1)\theta}(\sin{0.5(n+2)}\theta-\sin{0.5n\theta})$$

$$=2\sin{0.5(n+1)\theta}\cos{\frac{0.5(n+2)\theta+0.5n\theta}{2}}\sin{\frac{0.5(n+2)\theta-0.5n\theta}{2}}$$

$$=2\sin{0.5(n+1)\theta}\cos{0.5(n+1)\theta}\sin{0.5\theta}$$

$$=\sin(n+1)\theta \sin{0.5\theta}$$

PolymorphismPrince
  • 744
  • ??? Where do we get the (n+2) if we are assuming n = k+1 (or just n => n+1) – user71207 Nov 21 '20 at 07:09
  • I posted my attempt as an answer - would you be able to have a look? – user71207 Nov 21 '20 at 07:29
  • @user71207 to understand what I have done in my hint, equate the first line with last line. Then add $\sin{0.5(n+1)\theta\sin{0.5n\theta}}$ to both sides and divide by $\sin{0.5\theta}$. Hopefully you will see then that I have shown exactly the algebra you need to complete your proof. – PolymorphismPrince Nov 23 '20 at 05:03