Are complicated systems more likely to be chaotic?

Question

Though the simple pendulum isn't chaotic, the double pendulum is. Is it true in general that more complicated differential equations are more likely to be chaotic than simple differential equations? There are many ways differential equations can be complicated, but these are some of the criteria I can think of:

No analytical solution
Nonlinear
Coupled
More variables

I know that there are complicated differential equations which aren't chaotic, but would you have more luck finding chaos in a simple or complicated differential equation?

To make sense of words like "likely" and "luck", you have to specify a probability measure on the set of all differential equations. Good luck! — Gerry Myerson, Nov 21 '20 at 06:13
Do you think the equation $x_{n+1}=ax_n(1-x_n)$ is complicated? — N74, Nov 21 '20 at 10:59
Good point, @N74 but OP is specifically asking about differential equations, not difference equations (recurrence relations). — Gerry Myerson, Nov 21 '20 at 11:07
no, but similarly can a linear differential equation be chaotic? — yellowgrass, Nov 21 '20 at 11:08
If you made that recursion equation simpler by making it linear it wouldn't be chaotic either — yellowgrass, Nov 21 '20 at 11:10

score 3 · Accepted Answer · answered Nov 23 '20 at 07:41

Yes.

First of all, for continuous-time systems, you need at least the following ingredients for chaos:

non-linearity
three dimensions (you need one positive, one zero and one negative Lyapunov exponent)

These conditions already imply a certain complexity – but not all systems fulfilling them are chaotic. One reason for this is that you may have strongly coupled dimensions or weak non-linearities. Thus, if you increase the number of dimensions or strength of non-linearities, you increase your chances to find chaos.

Moreover, consider a complex system consisting of many coupled subsystems, with some only driving. Here, it take only a single chaotic subsystem to render the entire dynamics chaotic.

This also holds empirically: Complex systems show larger chaotic bands, i.e., parameter regimes in which they are chaotic. For example, consider the following figure from this paper (which I co-authored):

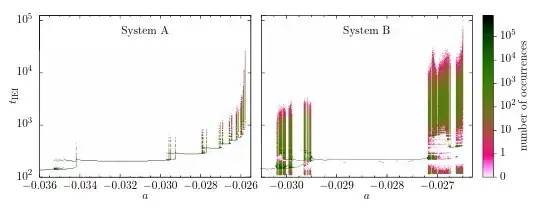
Systems B and A are coupled oscillator networks designed in the same way, except that System B has more components or dimensions, respectively. Whenever you see a vertical band in the diagram, you have chaos for that value of the control parameter $a$. As you can see, the chaotic regions are considerably larger for the more complex system.

No analytical solution

The solutions that are considered analytical are not chaotic. So this a also requirement for chaos, if you so wish.

Are complicated systems more likely to be chaotic?

1 Answers1