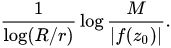Jensen's Formula and the number of zeros.

Question

I am doing a question that requires me to find the number of zeros in a disk when $f$ is non-constant, bounded and analytic on $D$. I saw that the Wikipedia page of Jensen's formula has the following information:

Jensen's formula can be used to estimate the number of zeros of analytic function in a circle. Namely, if f is a function analytic in a disk of radius R centered at $z_0$ and if |f| is bounded by M on the boundary of that disk, then the number of zeros of f in a circle of radius r < R centered at the same point $z_0$ does not exceed

Does anyone know how this formula is derived?

Answer 1

Let $f(z)$ be analytic function such that $f(0)\ne0$, and let $z_1,z_2,\dots,z_m$ denote the zeros of $f(z)$ satisfying $|z_k|<R$. Then Jensen's formula gives

$$ \int_0^1\log|f(Re^{2\pi it})|\mathrm dt=\log\left|f(0)\cdot{R\over z_1}\cdot{R\over z_2}\cdots{R\over z_m}\right| $$

Now, let $|f(z)|\le M$ for $|z|\le R$, then we have

$$ \log\left|{R\over z_1}\cdot{R\over z_2}\cdots{R\over z_m}\right|\le\log M-\log|f(0)| $$

Let $0<r<R$, so we can classify $z_1,z_2,\dots,z_m$ into two classes:

$$ \log\left|{R\over z_1}\cdot{R\over z_2}\cdots{R\over z_m}\right| =\sum_{|z_k|\le r}\log\left|R\over z_k\right|+\sum_{|z_j|>r}\log\left|R\over z_j\right| $$

Because $\log|R/z_k|$ is at least $\log R/r$, we have

$$ N(r)\log\frac Rr\le\sum_{|z_k|\le r}\log\left|R\over z_k\right| $$

where $N(r)$ denotes the number of zeros of $f(z)$ satisfying $|z|\le r$. Now, by the transitivity of inequalities, we conclude that the number of zeros of $f(z)$ within $|z|\le r$ satisfies the following inequality:

$$ N(r)\le{1\over\log R/r}\log\left|M\over f(0)\right| $$

Hope this will help you!

Answer 2

Lemma:

For an analytic $f$ with no zeros on $|z|=r$ and whose zeros inside $|z|=r$ are located at $\left\{\alpha_k\right\}_{k=1}^n$ with multiplicities, define $$ g(z)=f(z)\prod_{k=1}^n\frac{r^2-\bar\alpha_kz}{r(z-\alpha_k)}\tag1 $$ Then $|g(z)|=|f(z)|$ when $|z|=r$ and $g$ has no zeros in $|z|\le r$.

Proof:

The factors of $z-\alpha_k$ remove the zeros inside $|z|=r$, so $g$ has no zeros for $|z|\le r$.

If $|z|=r$, then $$ \begin{align} \left|\frac{r^2-\bar\alpha z}{r(z-\alpha)}\right| &=\left|\frac{\bar z}r\frac{r^2-\bar\alpha z}{r(z-\alpha)}\right|\tag{2a}\\ &=\left|\frac{\bar zr^2-\bar\alpha|z|^2}{r^2(z-\alpha)}\right|\tag{2b}\\ &=\left|\frac{r^2(\bar z-\bar\alpha)}{r^2(z-\alpha)}\right|\tag{2c}\\[6pt] &=1\tag{2d} \end{align} $$ Explanation:
$\text{(2a)}$: $|\bar z|=|z|=r$
$\text{(2b)}$: distribute $\bar z$ over the denominator
$\text{(2c)}$: collect the factors of $|z|^2=r^2$
$\text{(2d)}$: $|\bar z-\bar\alpha|=|z-\alpha|$

Thus, $\prod\limits_{k=1}^n\frac{r^2-\bar\alpha_kz}{r(z-\alpha_k)}$ has absolute value $1$ when $|z|=r$; and therefore, $|g(z)|=|f(z)|$ when $|z|=r$.

$\large\square$

---

Jensen's Formula

Taking the average over $|z|=r$ gives $$ \begin{align} \frac1{2\pi}\int_0^{2\pi}\log\left|f\!\left(re^{i\theta}\right)\right|\,\mathrm{d}\theta &=\frac1{2\pi}\int_0^{2\pi}\log\left|g\!\left(re^{i\theta}\right)\right|\,\mathrm{d}\theta\tag{3a}\\ &=\log|g(0)|\tag{3b}\\ &=\log|f(0)|+\sum_{k=1}^n\left(\log(r)-\log|\alpha_k|\right)\tag{3c} \end{align} $$ Explanation:
$\text{(3a)}$: the Lemma says $|g(z)|=|f(z)|$ when $|z|=r$
$\text{(3b)}$: the Lemma implies that $\log|g(z)|$ is harmonic for $|z|\le r$
$\text{(3c)}$: take the log of the absolute value of $(1)$ at $z=0$

$(3)$ is Jensen's Formula

---

Counting Zeros

If we know that all the zeros are inside $|z|=r$ and we know the average of $\log|f|$ on $|z|=R$, $$ \begin{align} \frac1{2\pi}\int_0^{2\pi}\log\left|f\!\left(Re^{i\theta}\right)\right|\,\mathrm{d}\theta-\log|f(0)| &=\sum_{k=1}^n\left(\log(R)-\log|\alpha_k|\right)\tag{4a}\\ &\ge n(\log(R)-\log(r))\tag{4b} \end{align} $$ So we have that $$ n\le\frac1{\log(R)-\log(r)}\left(\frac1{2\pi}\int_0^{2\pi}\log\left|f\!\left(Re^{i\theta}\right)\right|\,\mathrm{d}\theta-\log|f(0)|\right)\tag5 $$

Answer 3

We can obviously assume $z_0=0$, we also assume that $f$ doesn’t vanish on the circle of radius $r$ (not a big deal, we can take $r’> r$ small enough going to $r$).

Let $r < t < R$. Let $Z_t$ be the “set” of zeroes of $f$ in the disk centered at $z_0$ with radius $t$ (counted with multiplicity). We will make $t$ go to $R$ – we can choose $t$ such that $f$ does not vanish on the circle centered at $z_0$.

The exact Jensen formula, combined with the inequality $|f| \leq M$, gives $$\log{\frac{M}{|f(0)|}} \geq -\sum_{z \in Z_t}{\log{\frac{|z|}{t}}}=\sum_{z \in Z_t}{\log{\frac{t}{|z|}}} \geq \sum_{z \in Z_r}{\log{\frac{t}{|z|}}} \geq \sum_{z \in Z_r}{\log{\frac{t}{r}}}\geq |Z_r|\log{\frac{t}{r}}.$$

Now just take $t \rightarrow R$.