7

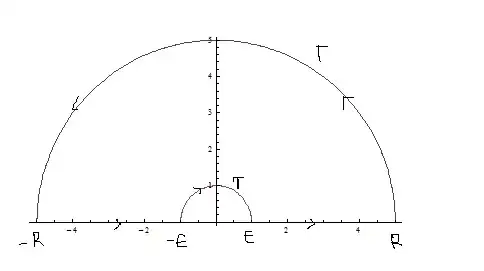
I am trying to integrate $\displaystyle \int_0^\infty \frac{\sin^2(x)}{x^2} dx$ by method of contour. I am considering the following contour but I am not being able to. Also I am not sure if it's right approach. contour

$$\int_\Gamma f(z) dz + 2 \int_0^\infty f(z) dz + \int_\gamma f(z)dz = 0$$ The first integral tends to zero as $R \to \infty $, but letting $\epsilon \to 0$, for the last integral I am getting. $$\int_{\pi }^0 \frac{\sin^2({\epsilon e^{i\theta}})}{\epsilon^2 e^{i2\theta }} i \epsilon e^{i\theta}d\theta = 0$$

ADDED:: Taking the above contour, we do not have any pole inside the contour. $$\int_{-\infty}^\infty \frac{1 - e^{i2z}}{2z^2}dz + \int_\Gamma \frac{1 - e^{i2z}}{2z^2} dz + \int_\gamma \frac{1 - e^{i2z}}{2z^2} dz = 0 \hspace{1 cm }(1)$$

$\displaystyle \int_\Gamma \frac{1 - e^{i2z}}{2z^2} dz \to 0$ due to Jordan Lemma. To evaluate $\displaystyle \int_\gamma \frac{1 - e^{i2z}}{2z^2} dz $ let the radius of the small semi circle be $\epsilon \to 0 $.

$$\lim_{\epsilon \to 0}\int_\pi^0 \frac{1 - e^{i2\epsilon e^{i\theta}}}{2\epsilon ^2 e^{i2\theta}} i \epsilon e^{i\theta}d\theta =\lim_{\epsilon \to 0} \int_\pi^0 \frac{1 - 1 - 2i\epsilon e^{i\theta} + O(\epsilon^2)}{2\epsilon e^{i\theta}} i = \lim_{\epsilon \to 0} \int_\pi^0 1+ O(\epsilon) d\theta = -\pi \hspace{1 cm }(2)$$

From $(2)$, $(1)$ reduces to $$\int_{-\infty}^\infty \frac{1 - e^{i2z}}{2z^2}dz - \pi = 0 \implies \Re \int_{-\infty}^\infty \frac{1 - e^{i2z}}{2z^2}dz = \int_{-\infty}^{\infty}\frac{\sin(x)^2}{x^2}dx = \pi$$

Including singularity at $z = 0$, we will have that small inner circle on lower plane. $$\int_{-\infty}^\infty \frac{1 - e^{i2z}}{2z^2}dz + \int_\Gamma \frac{1 - e^{i2z}}{2z^2} dz + \int_\gamma \frac{1 - e^{i2z}}{2z^2} dz = 2 \pi i \text{Residue}[f(z), z = 0] = 2\pi \hspace{1 cm }(3)$$

As for $\displaystyle \int_\gamma \frac{1 - e^{i2z}}{2z^2} dz = \lim_{\epsilon \to 0}\int_{-\pi}^0 \frac{1 - e^{i2\epsilon e^{i\theta}}}{2\epsilon ^2 e^{i2\theta}} i \epsilon e^{i\theta}d\theta = \pi \hspace{1 cm }(4)$

From $(3)$ and $(4)$ we get the same result.

Mula Ko Saag
  • 2,177
  • 1
  • 23
  • 45
  • No need (informally) to take that detour around zero, since $$\lim_{z\to 0}\frac{\sin^2z}{z^2}=1$$so we're talking of a removable singularity... – DonAntonio May 13 '13 at 16:27
  • @DonAntonio I had encountered this type of contour in $\int_0^{\infty}\frac{\sin x}{x} dx = \frac{\pi}{2}$, so I considered it might work := – Mula Ko Saag May 13 '13 at 16:29
  • Of course it works but not with your function...:) Read my answer. – DonAntonio May 13 '13 at 16:36
  • 1
    @user17762: I disagree. I am sure if you scour the M.SE posts you will find something similar, but that isn't it. Besides, where in that post is this particular question being asked? And, even so, it is unfair to the OP, who may not be as sophisticated as you, to call this a duplicate just because the problem is attacked more generally. – Ron Gordon May 13 '13 at 16:48
  • @RonGordon Actually there is no sophistication in the linked question. achille hui proves the general case using a similar if not the same contour. –  May 13 '13 at 16:53
  • @user17762 honestly that is too freaking complicated for a beginner like me :(( – Mula Ko Saag May 13 '13 at 17:03
  • 2
    This question shouldn't be closed since the other option is wa too advanced and general for a beginner. I'm voting to reopen. – DonAntonio May 13 '13 at 17:36
  • This integral appeared in http://math.stackexchange.com/questions/13344/proof-for-an-integral-involving-sinc-function – TCL May 13 '13 at 18:46
  • @TCL the last answer by joriki is I am looking for. which did not understand as I mentioned in comments. – Mula Ko Saag May 13 '13 at 18:47
  • Hi! Well.. I think your "added" should have been an answer =). – Physicist137 Sep 15 '16 at 18:45

2 Answers2

2

What you try to do won't work since your function is (almost) analytic insde the path you take and thus won't help you to evaluate the real integral.

Let us try the following:

$$\cos 2x=1-2\sin^2x\implies \sin^2x=\frac{1-\cos2x}{2} \;\text{define}\;\;f(z):=\frac{1-e^{2iz}}{2z^2}:$$

$$\text{Res}_{z=0}(f)=\lim_{z\to 0}\,zf(z)=\lim_{z\to 0}\frac{1-e^{2iz}}{2z}\stackrel{\text{l'Hospital}}=-i$$

Question: The above implies $\,z=0\,$ is a simple pole...why is this so and not a double one?

Taking your contour, taking the limits and etc. and using the lemma and, specially, its corollary in the 2nd. answer here , we get after comparing real and imaginary parts

$$\int\limits_{-\infty}^\infty\frac{\sin^2x}{x^2}dx=\pi\;\;\ldots\ldots$$

Community
  • 1
DonAntonio
  • 211,718
  • 17
  • 136
  • 287
  • Actually, it won't work because $\sin^2{z}$ does not converge on the outer contour. – Ron Gordon May 13 '13 at 16:38
  • @RonGordon, are you talking of my answer or of the intent the OP made with the function $,\frac{\sin^2z}{z^2},$ ? – DonAntonio May 13 '13 at 16:40
  • 2
    I am speaking of the first line in your answer: "What you try to do won't work since your function is (almost) analytic insde the path you take and thus won't help you to evaluate the real integral." $\sin^2{z}$ has a component of $e^{-i 2 z}$ which does not behave nicely on the outer contour of radius $r$ as $r \to \infty$. That is why using the function $\sin^2{z}/z^2$ won't work. – Ron Gordon May 13 '13 at 16:42
  • Well, perhaps...I'm not that sure, yet the complex integral of this function on that contour is zero and that also doesn't usually help to solve real integrals by means of complex integration... – DonAntonio May 13 '13 at 16:44
  • 1
    If by "this function" you mean $\sin^2{z}/z^2$, you are wrong: the integral of this function over the above contour blows up as $r \to \infty$. You need to take the piece you specify in the upper half plane, and another piece $(1-e^{-i 2 z})/z^2$ in the lower half-plane. – Ron Gordon May 13 '13 at 16:51
  • how come removable singularity changed into pole of order $1$ ?? is it due to $\sin $ component since we introduced $e^{i2z}$ ?? – Mula Ko Saag May 13 '13 at 16:52
  • Also what kind of contour do I need? should i extend it a bit below upper half plane to include $(0,0)$ ... since there is singularity at the path. There is also a question which has no answers. http://math.stackexchange.com/questions/246701/contour-integral-with-singularity-on-the-contour – Mula Ko Saag May 13 '13 at 17:01
  • Perhaps it blows ( I didn't check that ), yet it still vanishes in the shown contour, @RonGordon (in case you were addressing me...) – DonAntonio May 13 '13 at 17:02
  • @MulaKoSaag, did you notice that you worked with one function and I did work with another function ? – DonAntonio May 13 '13 at 17:03
  • @DonAntonio yes I saw that, but still I can't visualize the picture of contour. There is a pole of order $1$ at $z=0$. What contour do I need to consider such that there is no singularity on the path. – Mula Ko Saag May 13 '13 at 17:05
  • @MulaKoSaag, please: since we have at least two different functions, when you say "there is a pole..." do write explicitly to what function you refer. – DonAntonio May 13 '13 at 17:12
  • $f(z) := \frac{1 - e^{i2z}}{z^2}$ this function has a pole of order $1$ at $z=0$. I found my answer here ,,, http://math.stackexchange.com/a/382975/69881,,, but I am having trouble understand joriki's answer. How does he transit from 4 - to - 5 step? – Mula Ko Saag May 13 '13 at 17:14
  • Yes @MulaKoSaag, that's precisely what I wrote: that the function I chose has a simple pole at $,z=0,$ ... – DonAntonio May 13 '13 at 17:17
  • @DonAntonio could you check update? – Mula Ko Saag May 13 '13 at 17:28
  • I already did, @Mula: Use the very same contour you chose at the beginning but with the function I used!! Then check carefully the link I wrote there and you get your answer at once. – DonAntonio May 13 '13 at 17:37
  • Could you explain one more thing? how did you change $f(z) := \frac{1-e^{i2z}}{z^2}$ to $f(z) := \frac{1-e^{iz}}{z^2}$. I am getting residue to be $2i$ – Mula Ko Saag May 13 '13 at 18:01
  • Thanks to your question about the change I discovered a huge blunder from the trigonometric identity. I already edited my answer, thanks. – DonAntonio May 13 '13 at 22:52
  • I think we can solve this without taking residue at $z = 0$ also. If we take residue at $z = 0$, then I think we will be taking that curve $\gamma $ will be on lower plane. Please check my working. – Mula Ko Saag May 15 '13 at 20:04
1

There is a more easier way From this Evaluating the integral $\int_0^\infty \frac{\sin x} x \ dx = \frac \pi 2$? We know that , $$\frac{\pi}{2} =\int_0^\infty\frac{\sin x}{x} dx = \int_0^\infty\frac{\sin 2u}{2u} d(2u) =\int_0^\infty\frac{\sin 2u}{u} du\\ = \underbrace{\left[\frac{\sin^2 u}{u}\right]_0^\infty}_{=0} +\int_0^\infty\frac{\sin^2u}{u^2} du =\color{blue}{\int_0^\infty\frac{\sin^2u}{u^2} du} $$

Given that, $\sin2x = 2\sin x\cos x=(\sin^2x)'$ and $\lim\limits_{x\to 0}\frac{\sin^2 x}{x^2} = 1$

Guy Fsone
  • 23,903