-1

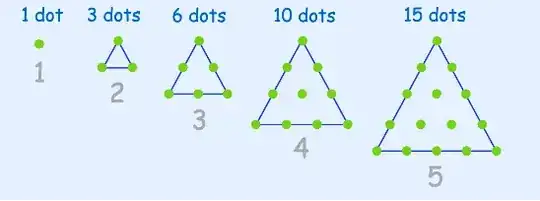
Prove by induction that the $n$-th triangular number is $\dfrac{(n(n+1))}{2}$. Triangular numbers are numbers that make a triangular dot pattern. enter image description here

Wolgwang
  • 1,563
bigred505
  • 3
  • 1
    @bigred Welcome to MSE! Note that askers are expected to provide context for their questions, as is explained here. For example, it would help if you could answer any of the following: what are your thoughts on the question? What have you tried so far? As far as the proof by induction looks like, can you write out the "base case" and "inductive hypothesis" statements? – Ben Grossmann Nov 11 '20 at 15:48
  • You must have a definition for "triangular number" that doesn't just consist of "forming a triangular dot pattern". A recursive definition like $T_{n+1} = T_n + n$ would be ideal. – Deepak Nov 11 '20 at 16:03
  • OK so Basically; (n) = 1,2,3,4,5 and T(n) = 1,3,6,10,15 and T(n) as a sum = 1, 1+2, 1+2+3, 1+2+3+4, 1+2+3+4+5 Ultimately now for example T(4)=1+2+3+4 – bigred505 Nov 11 '20 at 16:24
  • 1
    Does this answer your question? Proof $1+2+3+4+\cdots+n = \frac{n\times(n+1)}2$ – cosmo5 Nov 16 '20 at 18:46

1 Answers1

0

Let $P(n)$ denote the following statement.
The $n^{th}$ triangular number is $\frac{n(n+1)}{2}$.

Now the proof for $P(1)$:
$1^{st}$ trianular number is $\frac{1(1+1)}{2} =1$. So, $P(1)$ is true.

Let $P(n)$ be true. We'll prove $P(n+1)$ is true.
Firstly, note that $(n + 1)^{th}$ triangular number is $(n + 1) + n^{th}$ triangular number.

By this fact, and because $n^{th}$ triangular number is $\frac{n(n+1)}{2}$ (assumed), $(n + 1)^{th}$ triangular number is $n + 1 + \frac{n(n + 1)}{2} = \frac{(n + 1)(n + 2)}{2}$.

Hence, $P(n + 1)$ is true. And therefore the statement is true for all natural numbers.

Book Of Flames
  • 1,506