1

So, I just tried using Pythagoras theorem to prove: $\frac{d}{dx}\sin x= \cos x$ but it got me nowhere. Here is my work. $$\sin x= p/h.$$; where p and h are lengths of perpendicular and hypotenuse in a right angled triangle.

Differentiating w.r.t $x$, we get $$\frac{d}{dx}\sin x= \frac{1}{h^2} \left( h\frac{dp}{dx}-p\frac{dh}{dx}\right)\tag{i}$$

We know $h^2=p^2+b^2$. (Where b is the length of the base of the right angled triangle.) Differentiating w.r.t $x$, $$h\frac{dh}{dx}=p\frac{dp}{dx}$$ (If we put $b$ constant). Substituting in $(i)$,

\begin{align} \frac{d}{dx} \sin x&= \frac{1}{h^2} \left(h\frac{dp}{dx}-\frac{p^2}{h}\frac{ dp}{dx}\right)\\ & = \frac{1}{ph^2} \left(b^2\frac{dp}{dx}\right) \tag{ii} \end{align} Now, I lost track here because I didn't know how is that equal to $\cos x$. Can anyone help me continue from here?

(Note: I know how to derive this from first principle. I just wanted to try using Pythagoras theorem and trigonometric identities. I kept the base length constant because it appeared to me that if I changed the x, base length won't be effected. But as I can see in the answer, the hypotenuse remains constant. However, can we keep the base constant and end up getting the same result? Maybe not visualising a circle of radius h but just a right angled triangle whose base remains constant w.r.t the reference angle?

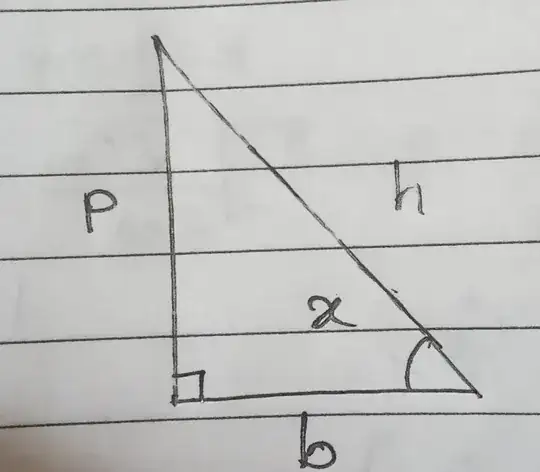
enter image description here

Ps: The called duplicate one is out of my understanding. I request a simpler version.

Akil
  • 203
  • Please use MathJax in your question. You will need to define $p, d, h$ for your question to make sense. – Toby Mak Nov 10 '20 at 10:32
  • Please add the definition of $h, p, b$. The claim that $b$ is constant is bugging me... – Arctic Char Nov 10 '20 at 10:55
  • My guess is that $h,p,b$ are the hypotenuse, perpendicular, and base of the right triangle. But you should state that explicitly in your question. I agree with @ArcticChar that it's a bit odd to make $b$ constant. You should be using triangles in the unit circle, i.e., with a constant hypotenuse of 1. – PM 2Ring Nov 10 '20 at 12:01

1 Answers1

1

So, the way to think about this is to recognize three important facts:

  1. On a unit circle, the hypotenuse will always be 1
  2. On a unit circle, the distance around the circle is the same as the angle in radians
  3. The change angle x, as the distance on the unit circle approaches zero, closer and closer approximates a LINEAR change

So, we will use $a$ for the adjacent, $p$ for the opposite, and $x$ for the angle in radians.

The definition of sine is $\frac{\text{opposite}}{\text{hypotenuse}}$ and the definition of cosine is $\frac{\text{adjacent}}{\text{hypotenuse}}$. Since the hypotenuse is $1$, this means that $\sin(x) = p$ and $\cos(x) = a$. The derivative of $\sin(x)$ with respect to $x$, therefore, is $\frac{dp}{dx}$. If we can show that $\frac{dp}{dx} = a$, then we win.

Okay, the pythagorean theorem (plus #1 above) gives us: $$ a^2 + p^2 = 1 \\ p^2 = 1 - a^2 $$

Differentiating yields: $$2p\,dp = -2a\,da \\ dp = -\frac{a}{p}da \\ da = -\frac{p}{a}dp$$

Now, because of #2 and #3, we can use the distance formula to say: $$dx = \sqrt{dp^2 + da^2} \\ dx = \sqrt{dp^2 + (-1)^2\frac{p^2}{a^2} dp^2} \\ dx = \sqrt{dp^2 + \frac{1 - a^2}{a^2} dp^2} \\ dx = \sqrt{dp^2 + \frac{dp^2}{a^2} - dp^2} \\ dx = \sqrt{\frac{dp^2}{a^2}} \\ dx = \frac{dp}{a}$$

So, this means that we can transform $\frac{dp}{dx}$ like this: $$ \frac{dp}{dx} = \frac{dp}{\frac{dp}{a}} = \frac{dp}{1}\frac{a}{dp} = a$$

QED

johnnyb
  • 3,509