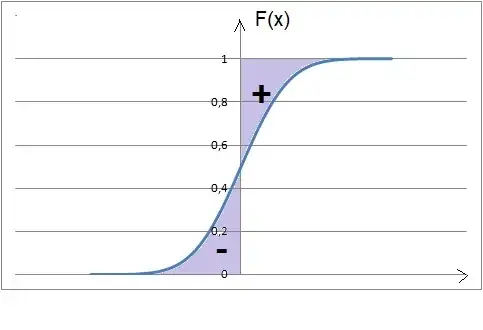
Show that any discrete or continuous random variable $X$ satisfies $E(X) = \int_{0}^\infty P(X > x)dx - \int_{0}^\infty P(X < -x)dx$

Question

Show:
$$E(X) = \int_{0}^\infty P(X > x)dx - \int_{0}^\infty P(X < -x)dx$$

$E[X]$ is the expectation value of the Random Variable $X$
$P$ is the probability

We know
$$E(X) = \int_{-\infty}^\infty xf(x)dx$$ $$f(x)dx = \frac{\mathrm{d}}{\mathrm{d}x}P(X\le x)$$

So, $$ E(X) =-\int_0^\infty x\,\frac{\mathrm{d}}{\mathrm{d}x}P(X\le x)\,\mathrm{d}x $$

$$ E(X) =-\int_0^\infty x\,\mathrm{d}P(X\le x) $$ Using Integration by parts: $$ \mathrm{E}(X)=-\lim_{x\to\infty}x\,P(X\le x)+\int_0^\infty P(X\le x)\,\mathrm{d}x $$

However, I do not know how to proceed further. Help would be greatly appreciated.

The line after the definition of expectation is wrong. You should write $P(X > x)$ as an integral, and then visualise the integrating region of the resulting double integral on a graph, to see how you can proceed further. — Benjamin Wang, Nov 08 '20 at 17:22
@BenjaminWang thank you for the comments. I just made the edit. Does it work now? — Just another person, Nov 08 '20 at 17:26

tommik · Accepted Answer · 2020-11-08T17:58:48.440

Let's take the first integral (by parts)

$$\int_0^{+\infty}\mathbb{P}[X>x]dx=\int_0^{+\infty}[1-F_X(x)]dx=\underbrace{x[(1-F_X(x)\Big]_0^{+\infty}}_{=0}-\int_0^{+\infty}-xf_X(x)dx=\int_0^{+\infty}xf_X(x)dx$$

In fact

$$\lim\limits_{x \to +\infty}x[1-F_X(x)]=\lim\limits_{x \to +\infty}\frac{x}{\frac{1}{1-F_X(x)}}=\frac{+\infty}{+\infty}\xrightarrow{\text{Hôpital}}=\lim\limits_{x \to +\infty}\frac{1}{\frac{f_X(x)}{[1-F_X(x)]^2}}=\lim\limits_{x \to +\infty}\frac{[1-F_X(x)]^2}{f_X(x)}=0$$

With similar reasoning for the other integral you get

$$ \bbox[5px,border:2px solid black] { \int_0^{+\infty}\mathbb{P}[X>x]dx-\int_{-\infty}^{0}\mathbb{P}[X\leq x]dx=\int_{-\infty}^{+\infty}xf_X(x)dx=\mathbb{E}[X] \ } $$

Graphically, the expectation is the difference of the following areas

Thus you are all set!

score 0 · Answer 2 · answered Nov 08 '20 at 22:18

The following answer is useful if you know a little bit of integration theory as given in measure theory.

Of couse the formula only makes sense if $X$ is integrable, i.e. $\mathbb E|X|<\infty$. The result does not depend on the type of the distribution. Just note that $$\mathbb P(X>x)=\mathbb E[\mathbf{1}_{X>x}], \ \ \ \text{and} \ \ \ \mathbb P(X<-x)=\mathbb E[\mathbf{1}_{X<-x}]$$ Now we apply Fubini (we are allowed to apply Fubini since $X$ is integrable, check it!) $$\int^\infty_0 \mathbb E[\mathbf{1}_{X>x}-\mathbf{1}_{X<-x}]\,dx=\mathbb E\left[\int^\infty_0 \mathbf{1}_{X>x}-\mathbf{1}_{X<-x}\,dx\right].$$ Note that $$\int^\infty_0 \mathbf{1}_{X>x}\,dx=X\mathbf{1}_{X\geq 0},$$ and $$ \int^\infty_0 \mathbf{1}_{X<-x}\,dx=\int^\infty_0 \mathbf{1}_{-X>x}\,dx=-X\mathbf{1}_{X< 0} $$ So $$\int^\infty_0 \mathbb E[\mathbf{1}_{X>x}-\mathbf{1}_{X<-x}]\,dx=\mathbb E[X\mathbf{1}_{X\geq 0}+X\mathbf{1}_{X< 0}]=\mathbb E[X\underbrace{(\mathbf{1}_{X\geq 0}+\mathbf{1}_{X< 0})}_{=1}]=\mathbb E[X] $$

Show that any discrete or continuous random variable $X$ satisfies $E(X) = \int_{0}^\infty P(X > x)dx - \int_{0}^\infty P(X < -x)dx$

2 Answers2