Intuitive understanding of why the sum of nth roots of unity is $0$

Question

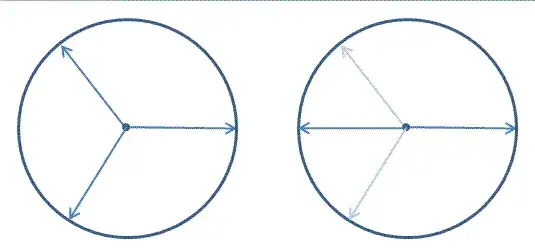
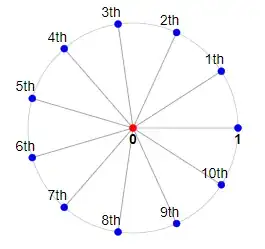
Wikipedia says that it is intuitively obvious that the sum of $n$th roots of unity is $0$. To me it seems more obvious when considering the fact that $\displaystyle 1+x+x^2+...+x^{n-1}=\frac{x^n-1}{x-1}$ and that $\{\alpha \in \mathbb{C}: \alpha^n=1\}$ is a cyclic group.

For me, it is hard to, intuitively, see this in the case that $n$ is an odd composite natural number.

Here is my reasoning thus far:

Let $n=5$. (I understand this is simple when considering the minimal polynomial).

Since the conjugate of an $n$th root of unity is also an $n$th root of unity, it is easy to see that, when written in trigonometric form, the sum (possible reordering here)

$1+\alpha^1+\alpha^2+\alpha^3+\alpha^4$

$=1+( \cos (72)+i \sin (72))+( \cos (144) + i \sin (144))+( \cos (72)-i \sin (72))+( \cos (144)-i \sin (144))$
$=1+2 \cos (72)+2 \cos (144)$.

Somehow $2 \cos (72)+2 \cos (144)=-1$, but I'm not sure this is obvious, or perhaps I'm being silly here.

What do you think? Silly?

Answer 1

The $n$ roots of unity of order $n$ (all of them, not just the primitive ones) are equally spaced around the unit circle. If their sum was nonzero, it would have an argument (angle relative to the $x$ axis) which would be a violation of symmetry. Therefore, by symmetry, the sum must be 0.

Answer 2

Consider the cube roots of unity. You can write them in the plane with $x$ being the real part and $y$ being the imaginary part. They give three vectors all with unit length, equally spaced around the unit circle. Now let's add the two vectors that are not 1 (ie, the two that face to the left) and you get $-1$ as shown in the second picture below (the light vectors are gone and their sum is the left-pointing vector which represents $-1$). Of course you can add any two vectors you like, but it will always give you a vector that is the negative of the remaining one. Adding the final two will give 0. This happens for any number of vectors when they are a complete set of all roots of unity.

Note: This is far from a rigorous proof, but I'm trying to appeal to your intuition. The picture isn't nearly so nice for 5-ths roots of unity.

To address your edited question, yes, $2\cos(72) + 2\cos(144) = -1$. It's not obvious, so I don't think you're being silly. It comes from the general formula

$$ \sum_{k=1}^n \cos \frac{2 \pi k}{n} = 0 $$

which, with a tiny amount of manipulation, gives you the formula above. This identity gives another proof that the $n$-th roots of unity sum to 0: the $\sin$ values will cancel each other out leaving a cosine sum equivalent to the above. The normal proof for this formula uses complex numbers, but you can also obtain a more elementary proof using trig identities. However, I would argue that your request for an intuitive understanding is better served by the respondents using "center of mass" type arguments than this trigonometry stuff.

Answer 3

Appealing to physical intuition, it is just the center of mass.

Think of the roots of unity as the coordinates of $n$ identical balls equally spaced around a circle in $\mathbb{R}^2$. What is the location of the center of mass? It is the center of the circle. Consequently, adding the roots of unity gives the center of the unit circle, which is $0$.

Answer 4

Here's an algebraic version of Alon's comment, basically your initial argument hopefully written more-intuitively: the $n$ roots are $1, \zeta, \zeta^2, \ldots, \zeta^{n-1}$ where $\zeta$ is a primitive $n$th root ($\zeta^n=1$). Let $S$ be the sum of all of these: $S=1+\zeta+\zeta^2+\ldots = \Sigma_{i=0}^{n-1} \zeta^i$. Then $\zeta S = \zeta+\zeta^2+\ldots+\zeta^n = \zeta+\zeta^2+\ldots+\zeta^{n-1}+1 = S$; rotating so that the zero'th root becomes the first, the first becomes the second, etc. - that is, multiplaying by $\zeta$ - can't change the sum.

Answer 5

If $\rm\:n>1\:$ then $\rm\:x^n - b\ x^{n-1} + \cdots\:$ has root sum $\rm\:= b\:,\:$ hence $\rm\:x^n - 1\:$ has root sum $= 0\:.$

At the heart of the matter is the following addition law:

$$\rm\ \ \ (x^k-{\color{red} r}\ x^{k-1}+\cdots\:)\ (x^n - {\color{red} s}\ x^{n-1}+\cdots\:)\:\ =\ \ x^{k\:+\:n} - ({\color{red}{r+s}})\ x^{k\:+\:n-1} + \cdots$$

Answer 6

There's another intuitive explanation I haven't seen mentioned yet. If you start at the origin and draw a regular $n$-gon with side length 1, starting by going from $(0,0)$ to $(1,0)$ and then proceeding counterclockwise, then the vector corresponding to the $k$th side is exactly $\zeta^{k-1}$. But since the $n$-gon ends out back at the origin, the sum of all these vectors is exactly $0$. Thus the sum of all $n$th roots of unity must be zero.

Answer 7

While you often find depictions of the sum of roots of unity like this

which help you understanding why the sum is zero (see user Fixee's answer above).

I find this depiction even more intuitive and straightforward. It works as a proof without words somehow, and it works for arbitrary $n$:

Answer 8

Think of the roots of unity $1,\omega,\dots,\omega^{n-1}$ as two-dimensional vectors that lie on a regular $n$-gon. If you rotate all of these vectors by $(2\pi)/n$ radians about the origin, then the shape is unchanged. Let $T:\mathbf R^2\to\mathbf R^2$ be the linear transformation that represents this rotation. We have $$ \sum_{k=0}^{n-1}\omega^k=\sum_{k=0}^{n-1}T(\omega^k)=T\left(\sum_{k=0}^{n-1}\omega^k\right) \, . $$ Assuming that $n\ge2$, the only invariant point of $T$ is $\mathbf 0$, and so it must be the case that $\sum_{k=0}^{n-1}\omega^k=\mathbf 0$.