3

EDIT: Answer added.

I haven't slept much lately and I've been raging on this thing for a couple hours now. I really hope some people here can have the same obsession/rage and will help me out.

I have two sets, A and B. |A| = m, |B| = n. I was looking for the number of surjections from A to B, and I found a formula here: http://www.ma.utexas.edu/users/kbi/COURSES/TERM/11S/325K/L17.pdf

I seem to have understood the following:

You have to calculate the Stirling number of the second kind, and then multiply it with n! due to the fact that Stirling numbers only divide/group (and do not map). I have the following in maple:

f:=(n,m)->n!/(m!*(n-m)!);

test:=Sum((-1)^if(n,n-i)(n-i)^m,i=0..n);

If I set m to be 500 and n to be 300, then test > n^m, the latter being the total number of functions. The number of surjective functions is a subset of the number of functions and should therefore not be higher. My blood is boiling, because I know I'm overseeing something idiotic. Hoping for help.

EDIT:

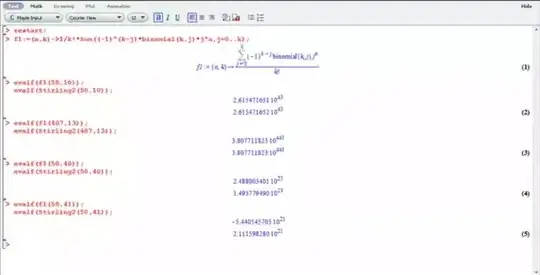
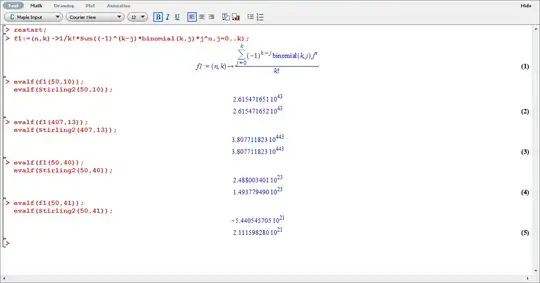
Not sure what the protocol is on adding answers, but this question has been answered. It is most likely a problem with maple. I added a screenshot of my maple worksheet. I defined a function f1(n,m) myself, that acted odd. I googled and found that maple has a default implemented Stirling2(n,m) function. As the screenshot shows, both functions give the same result for many values of n and m, but not for all. Apparantly I need 10 rep to post images, so I'll link to imgur: enter image description here

Wolgwang
  • 1,563
jvanheesch
  • 31
  • There are no surjections from a $300$-element set onto a $500$-element set. You need to have $m\ge n$ to get any surjections at all. – Brian M. Scott May 12 '13 at 15:52
  • Well that sounds obvious of course - I'm not plain stupid it's just a temp thing. However, I don't see where I do that. I set m to be 500 and n to be 300, so m > n. Where did I do it wrong? Thank you in advance. – jvanheesch May 12 '13 at 15:54
  • My apologies: I inadvertently interchanged $m$ and $n$. Hang on, and I’ll take a closer look. – Brian M. Scott May 12 '13 at 15:55
  • Don't worry, they look very similar. I love you for your intentions, and I'd love you even more if you could find out what I'm doing wrong. – jvanheesch May 12 '13 at 15:56
  • I don’t use Maple, but I believe that it has a built-in binomial coefficient function, binomial(n,r); what happens if you use it instead of your $f$? – Brian M. Scott May 12 '13 at 16:11
  • Just changing the word binomial in 'test' and removing 'f:=...' gives the exact same thing. So no explanation yet, although less possibilities (i.e. the definition of f was not the cause). – jvanheesch May 12 '13 at 16:14
  • What (roughly) are the two numbers that you get? – Brian M. Scott May 12 '13 at 16:15
  • I made a screenshot. That way I cannot make any inconsistensies between what I type here and in maple. It's probably a very stupid mistake, but I just don't see it. http://i.imgur.com/SMT5VTg.png – jvanheesch May 12 '13 at 16:18
  • Do me a favor and run it with $m=50,n=30$; I’d like to see the two numbers for that smaller case. – Brian M. Scott May 12 '13 at 16:23
  • I made two; one with m = 50, n = 30 and one with m = 50, n = 45. In the latter one, test turns out negative. http://i.imgur.com/IwNk0sy.png – jvanheesch May 12 '13 at 16:29
  • Something’s clearly wrong with the evaluation of test: there’s no way that it should be negative. The correct value with $n=45$ is about $1.570978205708\times 10^{69}$, according to this and my calculator, which says that $45!\approx1.196222208655\times10^{56}$. – Brian M. Scott May 12 '13 at 16:36
  • Are you suggesting there's a chance maple's wrong? Or is there anything I might be doing wrong? – jvanheesch May 12 '13 at 16:39
  • The expression that you’re using looks right, and it’s giving a reasonable value when $n=30$, but it’s giving nonsense when $n=45$ and in the original problem. That looks to me like a problem with Maple, probably loss of precision, but I really don’t know anything about Maple. – Brian M. Scott May 12 '13 at 16:46
  • Would you mind calculating the values for m = 450 and n = 365? Those were the values I needed a solution for, but I'm unable to get them with maple. – jvanheesch May 12 '13 at 16:48
  • I’m sorry, but those are too big for any tool that I have available. – Brian M. Scott May 12 '13 at 17:03
  • Ah, yeah figured that would be possible. I'll try to get access to matlab somewhere, thank you a lot for your help. – jvanheesch May 12 '13 at 17:07
  • I take that back: Wolfram|Alpha gives reasonable-looking result; it’s a very small fraction of $300^{500}$. (I’m still not used to having a high-speed connection, without which W|A is nearly unusable.) – Brian M. Scott May 12 '13 at 17:09
  • Of course I meant of $365^{450}$; the fraction is about $1.91679\times10^{-88}$, according to W|A. – Brian M. Scott May 12 '13 at 17:16
  • Thank you very, very much. I did not know how to use W|A. It was the order of magnitude I was expecting. Not sure if my solution will be correct (riddle), but at least I can drop it now and start studying. – jvanheesch May 12 '13 at 17:24
  • If you have found the answer, you are encouraged to write up the answer in the answer box and (then if nobody gives a better one soon) accept it. That will save the answer and prevent unanswered questions. This is discussed here – Ross Millikan May 13 '13 at 22:26
  • Like this? Can only accept it in 17 hours though. Does editing bump my original post? Thank you for the help. – jvanheesch May 13 '13 at 22:39

1 Answers1

0

This question has been answered. It is most likely a problem with maple. I added a screenshot of my maple worksheet. I defined a function f1(n,m) myself, that acted odd. I googled and found that maple has a default implemented Stirling2(n,m) function. As the screenshot shows, both functions give the same result for many values of $n$ and $m$, but not for all.

enter image description here

JRN
  • 6,566
jvanheesch
  • 31
  • If you have a problem with Maple like this, you might want to contact Maple technical support. At the very least, they should be grateful for you finding a bug. – Sam Lisi May 14 '13 at 00:29