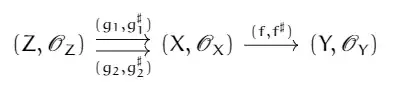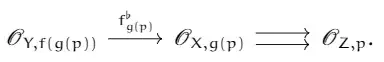I am trying to understand Tennison / Hitchin's Sheaf Theory proof of the following result.
Let $f:X\to Y$ be a morphism of ringed spaces such that the underlying map of topological spaces is a monomorphism and the morphism $f^\sharp:\mathscr{O}_Y\to f_\ast \mathscr{O}_X$ is an epimorphism. Then $f$ is a monomorphism in the category of ringed spaces.
The proof begins like this: (this is not a citation, it's just what I understood)
Let $(g_1,g_1^\sharp),(g_2,g_2^\sharp):(Z,\mathscr{O}_Z)\to (X,\mathscr{O}_X)$ be morphisms of ringed spaces such that the diagram
commutes. Passing to the diagram of underlying continuous maps, we get that $g_1=g_2$. Henceforth, we'll denote both $g_1$ and $g_2$ by $g$. By the adjunction between direct and inverse images, the diagram of sheaves over $Z$
is also commutative. Finally, passing to the stalks we obtain the commutative diagram
The authors then affirm that, by hypothesis $f^\flat_{g(p)}$ is an epimorphism. I can't see why that is true. The answer Relation between $\mathcal{O}_Y\rightarrow f_*\mathcal{O}_{X}$ and $f^{-1}\mathcal{O}_Y\rightarrow \mathcal{O}_X$ being epimorphism/monomorphism. even shows that this exact adjunction does not preserves epimorphisms. What am I missing?