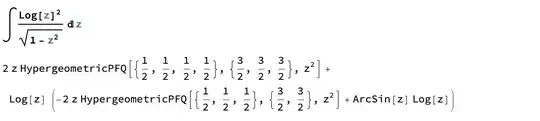In my favorite CAS is has two identic forms integrate in the sense of an unbounded general integral. I can only do screenshots because the MathML is ill-posed. This can be looked up in books with integreal relationsships and representations like Abramovitch, Stegun.
First a longer one:

Now are either integration done automatically or looked up in formula collections.
Evaluating this at the limits of the given integral is:
+∞
doubly singular. The signs do not change for -/+ . So the limits have to be taken. These are not too easy and need complex theory and residue methodology.
The problem gets simpler with the substitution t=x/2 and the knowledge that the function is even.

For t=0 and t=/2 the term is positive ∞.
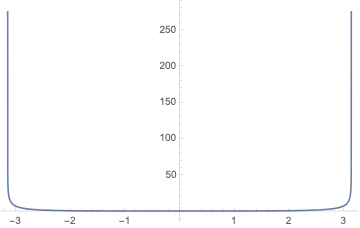
This is the graph of the function of the question:
With the substitution z=Cos[t] from @z-ahmed we get something even easier:
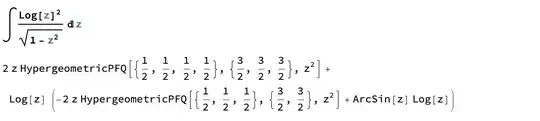
The process path can be gone in this direction and reverse. Mind the minus sign.
Our limit for z->0 is now 0.
The limit for z->1 is 1/24 (^2 + 3 Log5^2)
We remember our factor 4.
So the result is
 .
.
This can be simplified with 4 Log[2]^2 - Log[4]^2==0.