2

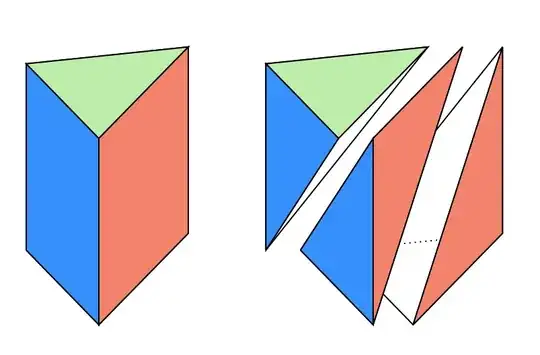
I read in a book a few months ago that the volume of a (solid) pyramid with a base that is ANY polygon (I'm not sure if it mentioned it being regular or not) is equal to $$\frac{1}{3}\times A\times h$$ where $A$ is the area of the base (i.e. of the polygon) and $h$ is the height of the pyramid.

This seems to be true in many cases, such as when the base is a square, a triangle and when the base is a circle (ie the pyramid becomes a cone).

My question is, how can we prove this? I simply have no idea.

Thank you for your help.

A-Level Student
  • 6,520
  • 1
    Similar, but not exactly your question: https://math.stackexchange.com/questions/623/why-is-the-volume-of-a-cone-one-third-of-the-volume-of-a-cylinder. Note the comment by Jamie Banks outlining a proof via calculus, which applies to any arbitrary base. – player3236 Oct 29 '20 at 17:59

2 Answers2

3

Any polygon can be decomposed into triangles, giving $A = A_1 + \cdots + A_n$.

Thus, $$\begin{align} V &= V_1 + \cdots + V_n\\ &=\frac13A_1h + \cdots + \frac13A_nh\\ &=\frac13(A_1 + \cdots + A_n)h\\ &=\frac13Ah. \end{align}$$

For the base case, you can decompose a prism like so. To see that the three pyramids have the same volume, note that the left and middle pyramids share a blue base and have the same height; similarly, the middle and right pyramids share a red base and have the same height.

enter image description here

Théophile
  • 24,627
  • 1
    I think you also have to prove that the volume of a triangular pyramid is $\frac{1}3Ah$ though. The OP wants the valid proof for all kinds of polygon bases including triangle. –  Oct 29 '20 at 17:59
  • @Student1058 Sure: in that case, simply decompose a triangular prism into pyramids. No integration is required. – Théophile Oct 29 '20 at 18:04
  • Thanks so much for your answer, it's beautiful in its simplicity! I'm not quite sure how you'd split a triangular prism into pyramids; would you mind elaborating please? – A-Level Student Oct 29 '20 at 18:09
  • @A-levelStudent Glad to help. I drew a picture illustrating the decomposition. – Théophile Oct 29 '20 at 18:33
  • Thanks for the illustration, I really appreciate it. So how exactly does that show that the volume of a triangular pyramid is $\frac{1}{3}Ah$? – A-Level Student Oct 29 '20 at 18:38
  • @A-levelStudent Given that the three pyramids all have the same volume, it follows that they each have a volume equal to a third of that of the prism, which is $Ah$. This is very similar to calculating the area of a triangle: cut a rectangle in a half along the diagonal, and, observing that the two resulting triangles have the same area, they must each be $\frac12wh$. – Théophile Oct 29 '20 at 18:43
  • Ah I see it now-thanks so much once again! Your diagram is really nice by the way; how did you make it? – A-Level Student Oct 29 '20 at 18:50
  • @A-levelStudent You're welcome! I did it in Inkscape, which is a freeware vector graphics program. – Théophile Oct 29 '20 at 18:52
2

For the most general case in which the base doesn't even need to be a polygon, it is an application of Cavalieri's Principle. Imagine a pyramid with a blob-shaped base and a square pyramid next to it with the same height and whose base has the same area as that of the first pyramid. Since any level cross-section of the two pyramids would have to have the same area, the volumes must also be equal.

There is a marvelous image showing that the area of a square pyramid whose height is equal to its base size and whose apex is above one corner of the base is 1/3 the volume of a unit cube. Long story short, you can construct three of those pyramids and see that they can be fit together to form a unit cube. From there, the only remaining step is to convince yourself that the volume of a pyramid whose base is a unit square is directly proportional to the height of the pyramid. At that point, you've proved it from a unit square pyramid with unit height to a unit square pyramid of arbitrary height to an arbitrary base and arbitrary height.