0

I have a question: Solve the following by deduction using backward reasoning to prove gt(5,2). I found from wikipedia that backward reasoning is same as backward chaining. Book says that backward chaining is same as goal dependent search. Suppose we are given the following facts:prove by deduction

Somebody please guide me. Sorry I don't have any idea. Should I try by doing the replacements provided at the end of each level of the tree? If somebody can help me I really appreciate.

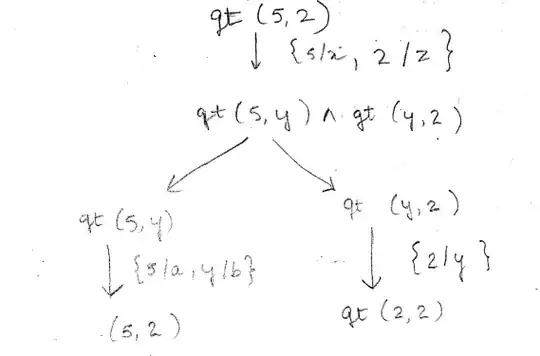
I got one solution from my friend. Kindly check it and explain if possibe. enter image description here

Linked concepts and Questions: By goal driven search it means that we have to start at the current state. How is it different from resolution proof?

Mauro ALLEGRANZA
  • 94,169
zak100
  • 177
  • Yes it is a Resolution proof: the negation of the statement to be proved, i.e. $\lnot g(5,2)$ has been added to the set of premises and the resolution proof procedure has to be applied. – Mauro ALLEGRANZA Oct 28 '20 at 06:53
  • Thanks for your response. I want to do deduction with backward reasoning instead of resolution proof, please guide me how we do backward reasoning/goal dependent search? How it is different from resolution proof? – zak100 Oct 28 '20 at 13:30

1 Answers1

1

See Backward chaining.

Regarding the handwritten proof sketch, the first step is to apply the substitution $\{ 5/x, 2/z \}$ to the clause in fact 1) to get:

$gt(5,y) \land gt(y,2) \to gt(5,2)$.

Thus, in order to prove $gt(5,2)$ (by Modus Ponens) we have to derive the antecedent: $gt(5,y) \land gt(y,2)$.

This is the new goal, that we split into: $gt(5,y)$ and $gt(y,2)$.

Consider the first one: $gt(5,y)$. Using again fact 1) with substitution $\{ 5/x, y/z \}$ we get: $gt(5,y) \land gt(y,y) \to gt(5,y)$.

The new goal is:

$gt(5,y) \land gt(y,y)$.

But the third fact is: $\forall x \lnot gt(x,x)$.

Thus, there is no way to derive $gt(y,y)$.

Mauro ALLEGRANZA
  • 94,169