Why is an element that belongs to a set that belongs to another set not an element of the second set?

Question

If $A \in B$ and $a \in A$, does $a \in B$? I've been told it does not. Why does it not?

For example, $ 1 \in \mathbb{N} \in $ S={subsets of $\mathbb{R}$}, but $1 \notin S$. — Adam Rubinson, Oct 27 '20 at 15:55
This may help: https://math.stackexchange.com/questions/2620616/what-is-the-difference-between-x-and-x-when-x-itself-is-a-set/2620621#2620621 — Ethan Bolker, Oct 27 '20 at 15:56
A human John is a citizen of New York: this can be written as $\text {John} \in \text {New York}$. Obviously NY is in US, and thus you are right. But there are cases when this is not true. NY belongs to the set of US cities. But $\text {John} \notin \text {US cities}$ because John is not a city. — Mauro ALLEGRANZA, Oct 27 '20 at 15:58
There is clear distinction in math (but not so clear in "human affairs") between $\in$ and $\subseteq$. Going back to the example above, if we consider the "universe" of humans, both a City and a State are collection of humans. Thus, $\text {John} \in \text {New York}$ and $\text {New York} \subseteq \text {US}$, from which we can correctly conclude with $\text {John} \in \text {US}$ — Mauro ALLEGRANZA, Oct 27 '20 at 16:18

Adam Rubinson · Accepted Answer · 2020-10-27T17:02:31.117

1

How about:

There is a word document on "My Desktop"

The word document contains several pictures, one of which is a picture of a rabbit.

However, there is not a picture of a rabbit on My Desktop.

$$$$

This is hopefully a clearer illustration because you can see the word document is there when looking at "My Desktop". However, you cannot see the picture of the rabbit when looking at "My Desktop". In other words, the word document acts like a black box, which is what we have when it comes to sets.

$$$$

Addendum:

However, it must be noted that sets do not always have a "meaning" and a "purpose" behind them. Sets are mathematical objects and the most important thing is knowing the precise mathematical definitions of things related to sets, e.g. you should know the definition of member of, subset of, complement of, intersection, union etc. The "meaning" and "purpose" of sets, for most people, I imagine, is slowly illuminated to them, the more they work with sets.

edited Oct 27 '20 at 17:02

answered Oct 27 '20 at 16:27

Adam Rubinson

20,052

So is it fair to assume then we treat the subset as if it were opaque and we can't see inside it? Why is it helpful to make the subset opaque in that sense? – Benjamin Lee Schoemann Oct 27 '20 at 16:43
You can't see or access the inside the word document unless you double click on it. You ask, "why is opaqueness helpful?". But remember - if the word document was not opaque then you would see pictures of rabbits and everything inside all your Desktop Files on the Desktop, which would be a real pain. So black-boxing ("opaqueing") things is necessary for usefully categorising and compartmentalising things, and for giving a structure/ hierarchy. In the "sandwich in a bag in a box" example, the bag has a purpose (keeping the sandwich away from snotty tissues in the bag). – Adam Rubinson Oct 27 '20 at 16:54

score 1 · Answer 2 · answered Oct 27 '20 at 18:58

I found an intuitive solution that I'm happy with. If you have a set of Animals={Dog, Cat, Elephant, Bird} and you looked at Dog as a set of parts such as Dog={Ears, Legs, Tail, Eyes, Mouth} it would not make sense to say that Ears ∈ Animals because Ears are not an animal. Only when Ears are combined with Legs, Tail, Eyes, and Mouth do you get Dog. The full set of elements that make up Dog are Necessary to make an animal. Ears all on its own is not an Animal therefore it cannot be an element of the Set Animals. Thanks for everyone's help!

score 0 · Answer 3 · answered Oct 27 '20 at 15:53

0

Put a sandwich in a bag, and put the bag in a box. The box contains a bag.

Put a sandwich in a box. The box contains a sandwich.

answered Oct 27 '20 at 15:53

MPW

43,638

1

If you Put a sandwich in a bag, and put the bag in a box you wouldn't say that the sandwich is inside the box? In reality, the sandwich is in the box. Why do we make this distinction here? – Benjamin Lee Schoemann Oct 27 '20 at 15:55
Because "in" means one specific thing. If you drink a glassful of water, and you're standing on the floor, it doesn't mean that there is water on the floor. There is water in you, and you are on the floor. Similarly, you can't just choose to ignore the bag. – MPW Oct 27 '20 at 15:59
1

(Why am I suddenly both hungry and thirsty? Heh.) – MPW Oct 27 '20 at 16:00
I feel like we're getting closer to my confusion and I really appreciate your time and patience but let me ask in a different way. – Benjamin Lee Schoemann Oct 27 '20 at 16:02
1

If a bag contains a sandwich, and a box contains that bag why does the box not contain the sandwich? Why do we make this distinction? Why is it helpful to make a distinction between the sandwich being in the box and the sandwich being contained by the box? Hope I'm not being frustrating, and this is an understandable confusion. – Benjamin Lee Schoemann Oct 27 '20 at 16:05
That was going to be question I was about to ask, Benjamin. I agree it is confusing – Adam Rubinson Oct 27 '20 at 16:09
I like the water example, but I don't think the sandwich example is helpful. – PM 2Ring Oct 27 '20 at 16:31
2

I don't think this metaphor is helpful. I'd certainly say that the sandwich is in the box in the first example. – Jair Taylor Oct 27 '20 at 16:41
The difference is that in the second case you would be willing to eat the contents of the box, but probably not in the first case, unless you like the taste of bags. They are not the same. – MPW Oct 27 '20 at 16:55

Adam Rubinson · Answer 4 · 2020-10-27T16:36:22.953

0

For example, $ 1 \in \mathbb{N} \in $ S={subsets of $\mathbb{R}$}, but $1 \notin S$.

Also, in maths we have precise meanings for subset of and member of. You are conflating the two.

edited Oct 27 '20 at 16:36

answered Oct 27 '20 at 15:57

Adam Rubinson

20,052

What does S represent here? Thank you. – Benjamin Lee Schoemann Oct 27 '20 at 16:09
$S$ is the set of all subsets of $\mathbb{R}$. Here are three examples of subsets of $ \mathbb{R}: $ { $4,7,8$ } , $ [-4, 1) \cup $ {8}, { $ \ \frac{1}{n}: n \in \mathbb{Z} $} . So basically, any well-defined collection of members of $ \mathbb{R}$ written inside curly brackets is considered to be a subset of $ \mathbb{R}$. – Adam Rubinson Oct 27 '20 at 16:15
So note that in my answer, { $1$ } $ \in S $, but $1 \notin S $ – Adam Rubinson Oct 27 '20 at 16:21
Also, note that { {$1$} } is a subset of $S$, but {$1$} is not a subset of $S$. – Adam Rubinson Oct 27 '20 at 16:39

Jair Taylor · Answer 5 · 2020-10-27T16:58:49.507

Let $A = \{\{1,2\}, \{3,4\}\}$. By definition, the only elements of $A$ are those in the comma-separated list: $\{1,2\}$ and $\{3,4\}$. So $\{1,2\} \in A$ and $\{3,4\} \in A$ but $1 \notin A$. This is just true by definition; $\in$ is not a transitive relation in standard set theory. You can't justify this by appeals to intuition; it's just a rule of the game.

We (that is, the mathematical community) could define $\in$ so that it is transitive, but we don't, because it would not be very convenient. With the definition as it is, it's very easy to tell whether anything is an element of a comma-separated list: it has to be one of the things in the list. Otherwise, to say for sure that $x \notin A$ you would have to check whether there happens to be any $B \in A$ with $x \in B$, or any $B \in A$ with a $C\in B$ so that $x \in C$, etc., which would create a headache. With the standard definition, you can say that a set $\{A,B\}$ with $A \neq B$ has exactly two elements: $A$ and $B$, and no more.

score 0 · Answer 6 · answered Oct 27 '20 at 17:51

0

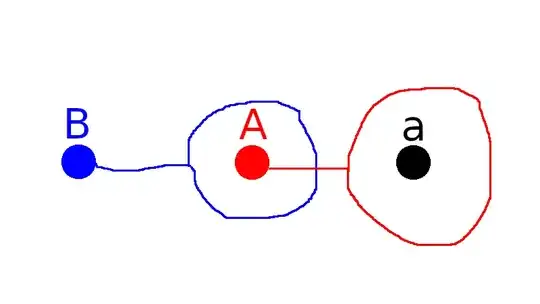
Actually, from just knowing that $A\in B$ and $a\in A$, you cannot decide whether $a\in B$ or not. Both situations are possible.

For example, consider the case that $A=\{a\}$ and $B=\{A\}=\{\{a\}\}$. This could be depicted as follows:

Here the dots denote the sets, and the loops enclose their elements. As you can see, the set $B$ (blue) contains the set $A$ (red), but not the element $a$ (black), as $B$'s loop does not enclose the dot $a$.

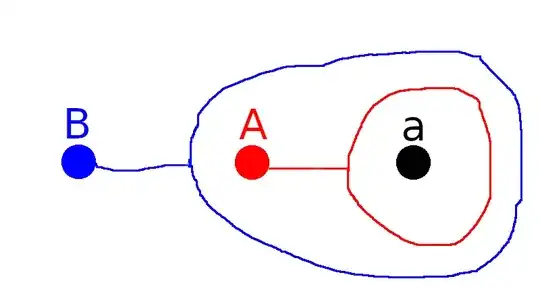
On the other hand, consider $A=\{a\}$ and $B=\{a,A\}=\{a,\{a\}\}$. Then $B$ does contain both the set $A$ and its element $a$. This can be depicted as follows:

As you can see, now $B$'s loop not only encloses the set $A$, but also the element $a$ (which is also enclosed by $A$'s loop).

But in both cases you have $A\in B$ (the dot $A$ is enclosed in $B$'s loop) and $a\in A$ (the dot $a$ is enclosed by $A$'s loop).

answered Oct 27 '20 at 17:51

celtschk

43,384

How can the set of A and the total elements that are contained by A be separate entities? By making them equal such as A={a} shouldn't they be interchangeable in the equation B={A} and then you substitute in the initial equation and get B={{a}}. Why does B={{a}} not necessitate that B={a}. – Benjamin Lee Schoemann Oct 27 '20 at 18:36
For instance if A had one entity a. We would denote that as A={a}. Why can we not also show that as A=a? – Benjamin Lee Schoemann Oct 27 '20 at 18:37
@BenjaminLeeSchoemann: In general, the elements of a set are not even an entity. For example, consider the set ${a,b}$. The elements are $a$ and $b$. Each of them is an entity, but $a,b$ is not. ${a,b}$ is an entity (is is the set containing $a$ and $b$ and nothing else), but it is not the same as the elements. Or consider the empty set. It is clearly an entity, but it contains nothing. Nothing clearly isn't an entity, or else it wouldn't be nothing. And finally, consider $A$ from above. It contains one element, $a$, but surely is not that element: ${a}\ne a$. – celtschk Oct 27 '20 at 18:58

Why is an element that belongs to a set that belongs to another set not an element of the second set?

6 Answers6