1

How to calculate the Fourier transform of $$f(x)=\frac{1}{|x+c||x-c|}$$ I tried using " https://www.wolframalpha.com/input/?i=Fourier+transform+calculator", but I don't get any results, please help me.

QFT addict
  • 81
  • Is it in dimension $1$ ? – LL 3.14 Oct 26 '20 at 17:51
  • You can easily restrict to $c=1$. Then you might get the result by writing $$ \mathcal F f = \mathcal F(|x^2-1|^{-1}) = \mathcal F(\mathrm{sign}(x^2-1),(x^2-1)^{-1}) $$ Now remarking that $\mathrm{sign}(x^2-1) = 1 - 2, \mathbf{1}{[-1,1]}$ you obtain $$ \mathcal F f = \mathcal F((x^2-1)^{-1}) - 2, \mathcal F(\mathbf{1}{[-1,1]},(x^2-1)^{-1}) $$ and you can get the first Fourier transform by https://math.stackexchange.com/questions/2909722/how-to-find-the-inverse-fourier-transform-of-fw-frac1w2-a2 and the second by https://en.wikipedia.org/wiki/Fourier_transform (Formula 501) – LL 3.14 Oct 26 '20 at 19:01
  • Depends on how you define $1/|x^2 - c^2|$. If you take it to be the distributional derivative of $$f(x) = \frac 1 {2 c} \ln \left| \frac {x - c} {x + c} \right| \operatorname {sgn} \frac {x - c} {x + c}$$ (which is a valid regularization of the ordinary function $1/|x^2 - c^2|$), then the FT is $-i w \mathcal Ff$. There is a closed form in terms of the sine integral and cosine integral functions. – Maxim Oct 27 '20 at 16:13

1 Answers1

1

Almost an answer, but with remaining questions...

First of all, this issue has to be considered in the sense of distributions.

Let us first concentrate on the F.T. of $1/|x|$ which is (see formula (2) in the detailed answer of @Sangchul Lee to this question:

$$\mathcal F (\tfrac{1}{|x|})=- \log|\xi| - (\gamma + \log(2\pi))\delta \tag{1}$$

where $\gamma$ is the Euler-Mascheroni constant.

Out of (1), it is immediate to obtain $\mathcal F (1/|x-c|)$ and $\mathcal F (1/|x+c|)$; it remains to convolve them, because a product is transformed into a convolution by $\mathcal F$.

Now, can we obtain a final closed form ? Maybe by working on the result obtained here ?

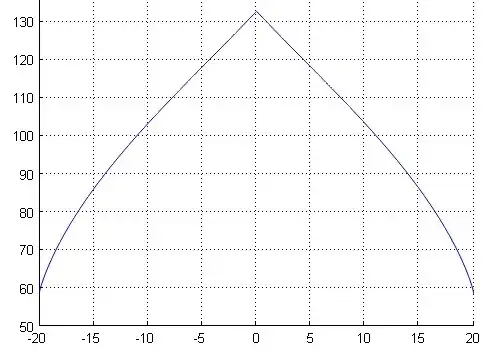
Using DFT, I have obtained the following ogival curve for this Fourier transform (code below); I will continue to work on this question ...

enter image description here

Matlab code:

x=-20:0.011:20;
c=1; % other values give almost the same shape
s=1./abs(x-c);u=fftshift(abs(fft(s)));
s=1./abs(x+c);v=fftshift(abs(fft(s)));
w=conv(u,v,'same');
plot(x,1e-7*w);

Remark: Wolfram Alpha, to the question phrased in this way: FourierTransform[1/Abs[x]], does provide an answer:

$$\tfrac{1}{\sqrt{2 \pi}} \int \tfrac{1}{|x|} e^{i\omega x}dx=-\sqrt{\tfrac{2}{\pi}}\left(\log(|\omega|)+\gamma\right)$$

The normalization factor $\tfrac{1}{\sqrt{2 \pi}}$ isn't an issue, we know it (it is one of the "avatars" of the Fourier Transform); but where have the $2 \pi$ and the dirac $\delta$ gone? ...

Jean Marie
  • 81,803
  • See the remark I just added. – Jean Marie Oct 25 '20 at 17:38
  • Thanks for your great effort, waiting for your more updated answer @Jean Marie – QFT addict Oct 25 '20 at 18:11
  • It does not seems there should be a Dirac delta (see for example my computations here https://math.stackexchange.com/questions/3723136/the-fourier-transform-of-1-p3/3724502#3724502). The $2\pi$ in the $\ln$ also depends on the normalization of the Fourier transform (since $\ln(2π x) = \ln(2\pi) + \ln(x)$) – LL 3.14 Oct 26 '20 at 17:49
  • Very interesting ! Yes, you are right: the $2 \pi $ term depends on the normalization, I should have thought about it. – Jean Marie Oct 26 '20 at 17:55
  • 1
    A way to be sure that there is no Dirac delta involved is just to remark that since $1/|x|$ is of homogeneity $-1$, its Fourier transform will be of homogeneity $1-1 = 0$ (if we are in dimension $1$) – LL 3.14 Oct 26 '20 at 17:56
  • New for me and interesting... – Jean Marie Oct 26 '20 at 17:58
  • 1
    Looking at the answer of Sangchul Lee you are refeering to, he is correct. But he is giving the Fourier transform of the $\ln$, in which you have a Dirac delta appearing. When you take the Fourier transform of his formula, you get what you tell, but replacing the delta by $\widehat{\delta_0} = 1$. So you just forget that ;) – LL 3.14 Oct 26 '20 at 18:01
  • In general, the convolution of two distributions with unbounded supports is undefined. – Maxim Oct 27 '20 at 16:19
  • 1
    @Maxim I recognize that I have some "holes" in my knowledge of distributions. Maybe, LL 3.14, could you answer ? – Jean Marie Oct 27 '20 at 16:33