It's not periodic, but large segments do repeat. You can work this out algebraically. First, note that the number of digits in a number $x$ is $\lfloor\log_{10}(x)\rfloor+1$ where $\lfloor \cdot \rfloor$ is the floor function, which rounds numbers down to the next integer below. This is because the first number with $2$ digits is $10^1$, the first with $3$ digits is $10^2$ and so on - so we can determine how many digits a number has by seeing which powers of $10$ it lies between.
In the case of the given function, we are really just plotting
$$\lfloor \log_{10}(2^x)\rfloor +1$$
over various $x$ - and bringing the exponent out of the logarithm gives that this is a plot of
$$\lfloor \log_{10}(2) \cdot x\rfloor + 1.$$
Note that, as $x$ gets very large, we have that the ratio $\frac{\lfloor \log_{10}(2) \cdot x\rfloor }x$ tends towards $\log_{10}(2)$ (which is irrational) since the floor function on top is irrelevant as the denominator grows. This rules out periodic behavior because if the graph were periodic, there would be some integer length of interval over which the function always increased the same integer amount - meaning the average rate of increase would be a rational (which is not the case).
That said, while it's a bit too much to write in a single answer, one can identify large segments that do repeat - the sequence of differences between consecutive values is known as a Sturmian word and has a lot of repeating behavior tied to the continued fraction of $\log_{10}(2)$ - the short of it is that the sequence $\lfloor c\cdot x\rfloor$ is periodic whenever $c$ is rational, but if $c$ is irrational, it is still very close to some rational numbers - which means that it behaves a lot like that rational number over some large period, but not forever.
To be a bit more explicit without getting too theoretical: the continued fraction of $\log_{10}(2)$ starts as
$$[0; 3, 3, 9, 2, \ldots]$$
The first term means that $\log_{10}(2)$ is approximately $1/3$ (but a little less), so we can get from that that the differences will always be composed of chunks of either $3$ or $4$ with a single increase per chunk - so every part of the graph looks like $0,\,0,\,1$ or $0,\,0,\,0,\,1$, where a $0$ means it stays flat and a $1$ means it increases.
In the next step, we start to put those little sequences together into bigger sequences - and the $3$ in the continued fraction essentially means that these terms will appear in blocks of $3$ or $4$ where one of the term $0,\,0,\,0,\,1$ term appears in each block. Numerically, this happens because $\log_{10}(2)$ is near $\frac{1}{3+\frac{1}3}=\frac{3}{10}$. The rest of the differences then are either in one of these patterns, built from the smaller patterns:
$$0,\,0,\,0,\,1,\,0,\,0,\,1,\,0,\,0,\,1$$
$$0,\,0,\,0,\,1,\,0,\,0,\,1,\,0,\,0,\,1,\,0,\,0,\,1$$
The next term would tell us that the larger blocks consist of $8$ or $9$ copies of the first pattern followed by one copy of the second pattern - and the sequence would continue being built in that manner. Note that this leads to large segments of repeating pattern that are eventually broken.
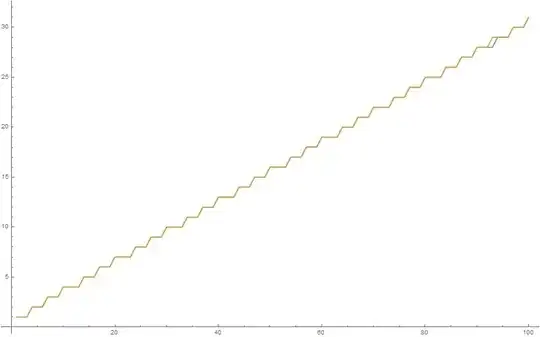
This sequence is not periodic because log(2)/log(10) is an irrational number. - T. D. Noe, Jan 10 2007– player3236 Oct 21 '20 at 17:16