I am stuck on this question below and was wondering if anyone could give me some hints on how to go forward.
-
1Do you know how to take the derivative of $a(x-r)(x-s)$? – Dave L. Renfro Oct 19 '20 at 16:35
-
@DaveL.Renfro do I just use the product rule? – realism98 Oct 19 '20 at 16:42
-
INteresting identity – tryst with freedom Oct 19 '20 at 16:48
-
2@Buraian Not really. The graph of a quadratic function has a strong symmetry and it is easy to see on it what the identity means (and why it is true). – TheSilverDoe Oct 19 '20 at 17:07
-
Understandable, have a nice day. – tryst with freedom Oct 19 '20 at 17:08
2 Answers
Method 1
$f'(x) = 2ax + b,\;$ so $\;f'(r) + f'(s) = (2ar + b) + (2as + b) = 2a(r+s) + 2b.$ Now recall that $r+s = -\frac{b}{a}$ (see here), which implies $b = -a(r+s),$ and hence we get
$$f'(r) + f'(s) \; = \; 2a(r+s) + 2b \; = \; 2a(r+s) -2a(r+s) \; = \; 0.$$
Method 2
If $r$ and $s$ are the roots, then both $x-r$ and $x-s$ are factors of $ax^2 + bx + c,$ which implies that $(x-r)(x-s)$ is a factor of $ax^2 + bx + c.$ Therefore, since $ax^2 + bx + c$ is quadratic $(r \neq s$ is needed here, but the result you want to prove is still true if $r$ is a repeated root) and $(x-r)(x-s)$ is quadratic, they differ only by a constant factor (unique factorization of polynomials; but it's likely you can assume this), which means we must have $ax^2 + bx + c = a(x-r)(x-s).$ Therefore, using the product rule, we have $f'(x) = a [1 \cdot (x-s) + (x-r) \cdot 1],$ and hence
$$ f'(r) + f'(s) \; = \; [(r-s) + (r-r)] \; + \; [(s-s) + (s-r)] \; = \; (r-s) + (s-r) \; = \; 0 $$ Incidentally, if you don't use the product rule, but instead expand $a(x-r)(x-s)$ first and then differentiate, you'll see $-a(r+s)$ show up as the coefficient of $x$ after expanding, and the details now look like those in Method 1.
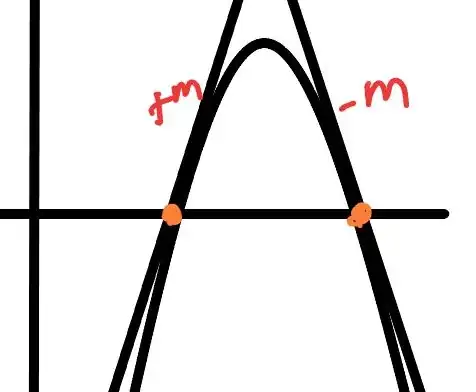
Geometric Interpretation
(courtesy of @TheSilverDoe's comment above)
The graph of $y = ax^2 + bx + c$ is a parabola whose axis of symmetry is the vertical line $x = \frac{r+s}{2},$ because the axis goes through the vertex and the vertex is (horizontally) midway between the two $x$-intercepts. Thus, the slopes (= steepness) at the intercepts (which are equi-distant from the axis) have equal magnitudes with opposite signs. It will help to draw a rough diagram. If the parabola opens upward, then the slope at the left intercept has a certain negative value, the slope at the right intercept has a certain positive value, and these two values have the same magnitude -- think about reflecting the left side of the parabola about the axis of symmetry to get the right side of the parabola. The situation is similar when the parabola opens downward.
- 11,538
- 36,843
-
-
If someone wants to include a diagram for the geometric interpretation, please go ahead. I'm not sure how to do this, and I don't really have time now anyway --- I'm busy with "day job" stuff that I temporarily put aside while writing this answer. – Dave L. Renfro Oct 19 '20 at 17:45
-
1
A quadratic function $f(x)$ can be written as $$f(x) = ax^2+bx+c = a(x-r)(x-s).$$ If we differentiate both sides and make use of the product rule we get $$f'(x) = a(2x-r-s).$$ Now write your desired expression and insert the zeros: $$f'(r)+f'(s) = a(2r-r-s)+a(2s-r-s) = a((r-s)+(-r+s)) = a\cdot0=0$$
- 432