Why is $\frac{X}{Y} = \frac{X}{\vert Y \rvert}$ for $X, Y \stackrel{\text{i.i.d}}{\sim} \mathcal{N}(0,1)$?

Question

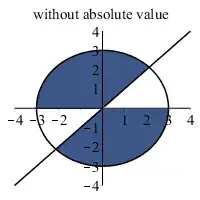
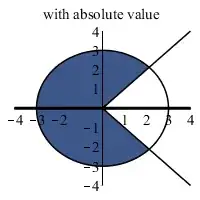
The justification provided was "symmetry of the Normal", but as far as I understand it $Y$ is not equivalent to $\lvert Y \rvert$, most obviously because the supports are no longer the same!

My Spidey-senses seem to suggest that it has something to do with the interaction of the signs of $X$ and $Y$ (being symmetric), but I can't quite put my finger on it. Below is my attempt to make sense of it in my head.

Thinking aloud (to hopefully illustrate my confusion/rationalization):

Suspending disbelief that densities aren't probabilities for a second (for intuition's sake), the proposition states that the likelihood of every value $\frac{X}{Y}$ is the exact same for the corresponding $\frac{X}{\lvert Y \rvert}$ (that equals $\frac{X}{Y}$).

Let's take $\frac{X}{Y} = 1$ (for concreteness), the following two disjoint events qualify (for all $t$ in $[-\infty, \infty]$):

• $X = t, Y = t$

or

• $X = -t, Y = -t$

...but if $\frac{X}{\lvert Y \rvert}$, the likelihood of a $+t$ in the denominator has doubled (and the likelihood of $-t$ has gone to $0$), but the likelihood of the numerator being $+t$ (so our ratio is $1$) is the same as it was without the absolute value in the denominator.

Rationalization: Since we've doubled our chances of seeing a denominator of $+t$ and the only remaining qualifying case is having both $X=t$ and $Y=t$ (since $\lvert Y \rvert \nless 0$) and $X, Y$ are independent, this precisely makes up for the loss of the second case above since $P(Y=t) = P(y=-t)$ from the symmetry of the normal.

---

Writing that out helped a lot...so I hope the reasoning is sound!

Answer 1

In distribution, they are the same. A realization of the random variable $Z_1=\frac{X}{Y}$ and of $Z_2 = \frac{X}{|Y|}$ each are distributed the same in absolute value. Also, the sign is distributed the same. $Z_1$ is positive half the time (when $\text{sign}X=\text{sign}Y$), and $Z_2$ is positive half the time (when $X$ is positive).

UPDATE

Looking at your answer within the question makes sense. Same idea.

Answer 2

$$\bigg\{\frac{X}{Y} \leq t\bigg\} = \{X \geq tY, Y < 0\} \cup \{X \leq tY, Y > 0\}$$ and $$\bigg\{\frac{X}{\lvert Y \rvert} \leq t\bigg\} = \{-X \geq tY, Y < 0\} \cup \{X \leq tY, Y > 0\}.$$

Since the above sets are disjoint, $$\mathbb{P}\bigg(\bigg\{\frac{X}{Y} \leq t\bigg\}\bigg) = \mathbb{P}(\{X \geq tY, Y < 0\}) + \mathbb{P}(\{X \leq tY, Y > 0\}) \tag{1}$$ and $$\mathbb{P}\bigg(\bigg\{\frac{X}{\lvert Y \rvert} \leq t\bigg\}\bigg) = \mathbb{P}(\{-X \geq tY, Y < 0\}) + \mathbb{P}(\{X \leq tY, Y > 0\}) \tag{2}.$$

Since $X$ and $Y$ are iid $\text{normal}(0,1)$, $$\mathbb{P}(\{X \geq tY, Y < 0\}) = \mathbb{P}(\{-X \geq tY, Y < 0\}).$$

To see the symmetry, consider the case $t = 1$ below. $(1)$ and $(2)$ above are obtained by integrating over the shaded regions.