Given the following graph
I gotta find the values of $r$ and $s$, with $r,s\in\mathbb{Z}$ such that they satisfy $$f(x)=|x-r|+|x-s|$$ I know the solutions are $2$ and $4$ but I don't know how to evaluate them. I tried to get the points of the graph but all I got was a system of modular equations, like $$\left\{\begin{array}{l}|r|+|s|=6 \\ |4-r|+|4-s|=2 \end{array}\right.$$ Are there elementary ways to solve this system or the problem itself?
By the definition of absolute value, you have
$$|y| = \begin{cases} y & y \ge 0 \\ -y & y \lt 0 \end{cases} \tag{1}\label{eq1A}$$
Thus, there are $4$ possible cases for what $f(x)$ is when removing the absolute values, depending on signs of $x - r$ and $x - s$. They are
$$f(x) = (x - r) + (x - s) = 2x - r - s, \; \text{ with } \; x - r \ge 0 \land x - s \ge 0 \tag{2}\label{eq2A}$$
$$f(x) = (x - r) - (x - s) = - r + s, \; \text{ with } \; x - r \ge 0 \land x - s \le 0 \tag{3}\label{eq3A}$$
$$f(x) = -(x - r) + (x - s) = r - s, \; \text{ with } \; x - r \le 0 \land x - s \ge 0 \tag{4}\label{eq4A}$$
$$f(x) = -(x - r) - (x - s) = -2x + r + s, \; \text{ with } \; x - r \le 0 \land x - s \le 0 \tag{5}\label{eq5A}$$
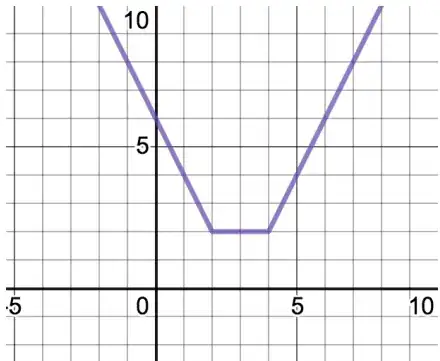
In the graph, the slope is $0$ (i.e., $f(x)$ is constant) only between $x = 2$ and $x = 4$. Thus, in that range, either \eqref{eq3A} or \eqref{eq4A} must apply. With \eqref{eq3A}, since $x - r$ is increasing with $x$, this gives $x - r \ge 0$ starts at $x = 2$, so $r = 2$. Similarly, this means $x - s \le 0$ ends at $x = 4$, giving $s = 4$. Substituting these into \eqref{eq3A} gives $-r + s = -2 + 4 = 2$, as required.
Note with \eqref{eq4A}, you get the reverse, i.e., $r = 4$ and $s = 2$. You can substitute these values into the definition of $f(x)$ to confirm they work properly.
Update: Note all the possibilities for $f(x)$ in \eqref{eq2A} to \eqref{eq5A} are of the form $f(x) = ax + b$ for various constants $a$ and $b$. This means the slope of the graph will be a constant and only change when the sign of $x - r$ and/or $x - s$ changes. Since the slope changes from $-2$ to $0$ at $x = 2$, this means one of $r$ or $s$ is $2$, while the slope changing from $0$ to $2$ at $x = 4$ means the other value of $r$ and $s$ is $4$.
The method I used originally is more general in that it can handle even unusual type cases, but this update shows how the somewhat simpler method can be used with your particular function instead.
