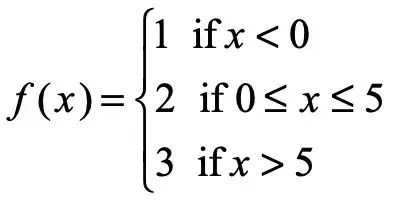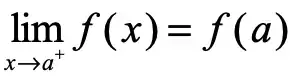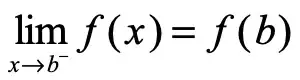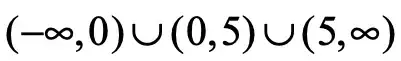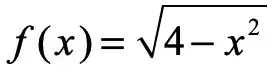1

enter image description here

I know that f is not continuous at 0 or at 5.

The definition of "f is continuous from the right at a" is:

enter image description here

Thus f is continuous from the right at 0.

The definition of "f is continuous from the left at b" is:

enter image description here

Thus f is continuous from the left at 5.

The definition of "f is continuous on the closed interval [a,b]" is that f is continuous on (a,b) and f is continuous from the right at a and f is continuous from the left at b.

Thus, by definition of continuity on a closed interval, f is continuous on the closed interval [0,5], since it is continuous on the open interval (0,5), continuous from the right at 0, and continuous from the left at 5.

If someone were to ask, "For what values of x is f continuous?" then I know that I would answer this, because f is discontinuous at 0 and 5:

enter image description here

But if someone were to say "Describe the intervals on which f is continuous," then how can I possibly dispute it if a student answers this?

enter image description here

We have in fact demonstrated that f is continuous on the closed interval [0,5], even though f is not continuous at either of the values 0 or 5.

My frustration is that as I have been combing the internet for example problems of continuity on closed intervals, I keep coming across examples like this, where f is not even defined outside of that closed interval:

enter image description here

But what about the example at the top of this post, where the function is defined beyond the closed interval in question, and is in fact discontinuous at the endpoints of that interval? Can we still say that f is continuous on that closed interval?

Frank Newman
  • 311
  • I do not see the problem here. The given function is discontinuous at 0 and 5. So it makes no sense to write that it is continuous in the closed interval $[0,5]$. – Cornman Oct 15 '20 at 14:39
  • I think what he's saying is that if the function was just $f(x)=2$ on the interval $0\leq x\leq5$, then that function would by definition be continuous on $[0,5]$. But somehow adding the other pieces makes the function discontinuous. I don't know how to resolve that. – DreiCleaner Oct 15 '20 at 14:43
  • This question may resolve what you asked about. The domain is important to consider. https://math.stackexchange.com/questions/1914931/is-sqrt-x-continuous-at-0-because-it-is-not-defined-to-the-left-of-0 – DreiCleaner Oct 15 '20 at 18:02
  • I want to reiterate this definition from my original posting: The definition of "f is continuous on the closed interval [a,b]" is that f is continuous on (a,b) and f is continuous from the right at a and f is continuous from the left at b. (1) Is that definition incorrect? (2) If it's correct, then isn't it the case that we must agree that f is continuous on [0,5]? – Frank Newman Oct 18 '20 at 17:19

0 Answers0