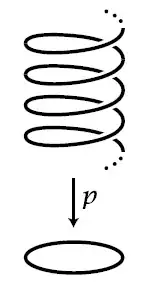First, let's work purely algebraically:
The elements of $\mathbb{Q} / \mathbb{Z}$ are the cosets $q + \mathbb{Z}$ for each rational $q \in \mathbb{Q}$. So $q_1$ and $q_2$ become equal if they differ by an integer. So we are considering $\frac{1}{2}$ and $\frac{3}{2}$, for instance to be the same. So for any $q \in [n, n+1)$ we can shift it to be in $[0,1)$ by subtracting $n \in \mathbb{Z}$. So we see that $\mathbb{Q} / \mathbb{Z}$ is exactly like $\mathbb{Q} \cap [0,1)$, where we work "mod 1". When we add $\frac{2}{3} + \frac{1}{2}$, we get $\frac{7}{6}$, which we reduce to $\frac{1}{6}$.
Geometrically, this is like "winding $\mathbb{Q}$ around a circle". It is at this point that I am legally required to show you this picture:
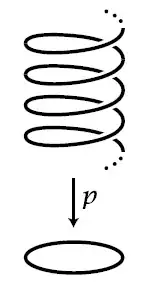
We are wrapping $\mathbb{Q}$ into a circle, so that two points in $\mathbb{Q}$ lie on top of each other exactly when their difference is an integer.
When you internalize these two perspectives, you should see why every element of $\mathbb{Q} / \mathbb{Z}$ has finite order. After all, if we start with $\frac{a}{b}$, and we add it to itself $b$ times, we'll be left with
$$
\underbrace{\frac{a}{b} + \frac{a}{b} + \cdots + \frac{a}{b}}_{b \text{ times}}
= b \frac{a}{b} = a = 0 \text{ (mod } 1)
$$
Now let's move to $\mathbb{R} / \mathbb{Q}$. This one is extra tricky, because there is no constructive way to choose an element from each coset. (There is some set-theoretic subtletly regarding the axiom of choice
Much ink has been spilled trying to understand this group (see
here and
here just to start), but I will give one "elementary" way to understand what is happening (though trying to visualize this group is going to be a mess no matter what you do). At the very least, this will let us resolve the question about infinite order elements.
We can write $\mathbb{R}$ as a Vector Space over $\mathbb{Q}$, and so (assuming choice) we can find a basis for $\mathbb{R}$ as a vector space. Just like every finite dimensional vector space over $\mathbb{R}$ looks like $\mathbb{R}^n$ for its dimension $n$, every infinite dimensional vector space over $\mathbb{Q}$ looks like $\mathbb{Q}^\kappa$ for its dimension $\kappa$.
So $\mathbb{R} \cong \mathbb{Q}^{\mathfrak{c}}$ (here $\mathfrak{c} = |\mathbb{R}| = \text{dim}(\mathbb{R}$) over $\mathbb{Q}$). Then when we quotient out by $\mathbb{Q}$, we can think about this as killing off one of the $\mathfrak{c}$ copies of $\mathbb{Q}$. Of course, since $\mathfrak{c}$ is infinite, we have (set theorists look the other way) "$\mathfrak{c} - 1 = \mathfrak{c}$". So we see that:
$$
\mathbb{R} / \mathbb{Q} \cong
\mathbb{Q}^{\mathfrak{c}} / \mathbb{Q} \cong
\mathbb{Q}^{\mathfrak{c}} \cong
\mathbb{R}
$$
Thus, by some nonconstructive black magic, $\mathbb{R} / \mathbb{Q} \cong \mathbb{R}$. But there is no way to describe the isomorphism more than we already have.
Like I said, though, this is enough information to answer your question:
Since every nonzero element of $\mathbb{R}$ has infinite order, so too does
every nonzero element of $\mathbb{R}/\mathbb{Q}$.
I hope this helps ^_^