I'd like to find a projective transformation that fixes the unit circle and sends some point on the $x$-axis within the unit circle to the origin (or I guess a random point in the unit circle, however, as I know that I can rotate, I thought this might be an easier case). Now, a fellow mathematician gave me a matrix that worked (under the assumption that we've already rotated our plane such that the remaining transformation works in the $XZ$-plane), but I had no idea how he got that matrix. He found $$ \begin{pmatrix} -\sqrt{1+c^2}&0&c\\ 0&1&0\\ c&0&-\sqrt{1+c^2} \end{pmatrix} $$ I know how to find some contraints; our conic is given by $x^2+y^2=z^2$, which corresponds to the diagonal matrix $D$ with $1,1,-1$ on the diagonal (in that order). So we're looking for a transformation $A$ which satisfies $A^TDA=D$. Furthermore, we'd like $A(x,0,z)=(0,0,z')$ for some $\vert x\vert<1$. But I'm kind of stuck how to derive the matrix above, or something similar. Any ideas?
1 Answers
A projective transformation that fixes the unit circle is an automorphic collineation in the Beltrami-Klein model of the hyperbolic plane. So this is the projective version of the better known automorphism of a unit disk as taught in complex analysis courses.
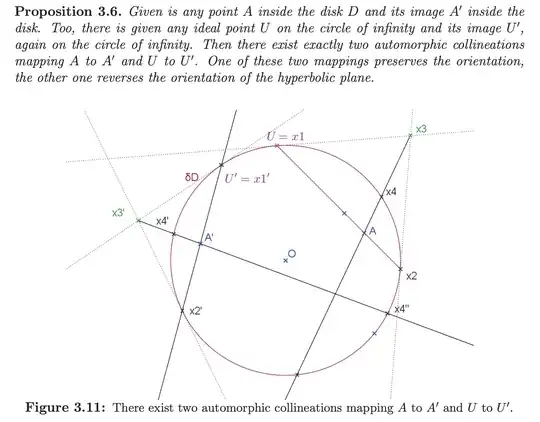
This is neither here nor there, but there is a handy practical guide Hyperbolic Geometry in Klein’s Model (by Franz Rothe) that can help with your question. In particular, the proof of Proposition 3.6 (pg 813) gives four source/target point pairs that define the projective transformation you want.
The URL (on the wayback machine) should be fairly stable, but here is the crux diagram:
Points $(x_1,x_2,x_3,x_4)$ map to $(x'_1,x'_2,x'_3,x'_4)$. Presumably you can derive a matrix from there, using math software or methods like this.
Addendum: OP asked what's meant by "counting with multiplicity, five points are mapped to other five points" in Rothe's proof. This is a shorthand for the scenario where two points on a curve converge to one and the chord they define becomes a tangent. You see it for example when the hexagon in Pascal's theorem degenerates to a polygon with less than 6 sides(e.g. page 4-5 here). In general, two tangents and three points will define 4 conics. But it will be unique if two of the points are on the tangents. A fuller discussion of the two tangents and three points case can be found in Pamfilos' A Gallery of Conics by Five Elements, Section 4.
- 8,626
-
Do you know what they mean by "counting with multiplicity, five points are mapped to other five points"? Which point would have multiplicity two, and what would that mean? – Sha Vuklia Oct 10 '20 at 19:20
-
A tangent counts as two points. A conic is determined by $\ell$ lines and $p$ points, where $\ell+p=5$. Because we're using $x_3$ (polar of $UA$) the mapping preserves the tangents at $x_1,x_2$. – brainjam Oct 10 '20 at 19:31
-
Amazing, thanks. – Sha Vuklia Oct 10 '20 at 20:03
-
Do you happen to have a source which proves that a tangent counts as two points? My literature is fairly limited, and I wouldn't like to dive into some higher (algebraic) geometry stuff, as I'm hoping the proof will be readable for second-year students. – Sha Vuklia Oct 10 '20 at 20:13
-
1See the Addendum in the answer. Hopefully it gives you the resources to cobble together an explanation/proof suitable for your students. I'm curious: is this for a course in projective geometry, or something else? – brainjam Oct 10 '20 at 21:08
-
Thank you! The course is called "Introduction to Geometry", which is meant as a broad introduction to mostly projective plane geometry for second-year math students. It's a short course (two months), so we can't go that much into depth, hence my question for a simple solution. With some help from this mathematician who gave me the matrix, I've managed to argue how to arrive at that matrix, without having to invoke Wolfram Alpha (or something similar), so for now I'll stick with that explanation, though I very much appreciated your efforts, as well as the sources/proofs you provided. – Sha Vuklia Oct 10 '20 at 22:47
-
I assume the matrix you gave is supposed to send $(c,0)$ to the origin. But that doesn't seem to be the case. Was there a typo or am I misunderstanding something? – brainjam Oct 11 '20 at 16:52
-
The matrix is supposed to send some point $(x,0)$ to the origin, which will determine the value of $c$. – Sha Vuklia Oct 29 '20 at 20:19