Prove that if two lines intersect and have direction vectors $\vec a$ and $\vec b$, their angle bisectors are always perpendicular to each other.
I know that if two vectors are perpendicular to each other they have a scalar product of 0. Would I have to then show that ($\vec a\ + \vec b$)⋅($\vec a\ - \vec b$) = 0 via parallelogram?
It is important that you first normalize vectors $\vec{OA} \, ( = \vec{a})$ and $\vec{OB} \, ( = \vec{b})$. Please see the below diagram as an example. The directional vector of angle bisector is in direction $OE$ but if you do not normalize the vectors, you will get a vector in direction $OF$.
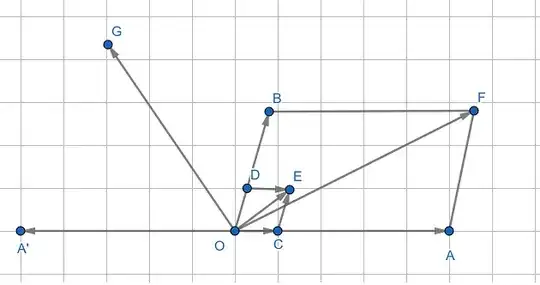
So, $\vec{OE} = \vec{OC} + \vec{OD}$
Unit vector $\vec{OC} = \displaystyle \frac{\vec{a}}{||a||}$
Unit vector $\vec{OD} = \displaystyle \frac{\vec{b}}{||b||}$
So, $\vec{OE} = \displaystyle \frac{\vec{a}}{||a||} + \frac{\vec{b}}{||b||}$
Directional vector for one of the angle bisectors = $\lambda_1 (||b|| \, \vec{a} + ||a|| \, \vec{b})$
Similarly the directional vector of the other angle bisector = $ \lambda_2 (||a|| \, \vec{b} - ||b|| \, \vec{a})$
Dot product of both angle bisectors = $\lambda_1 \lambda_2 \, (||b|| \, \vec{a} + ||a|| \, \vec{b}) \cdot (||a|| \, \vec{b} - ||b|| \, \vec{a}) = 0$
(as $\vec{a} \cdot \vec{a} = ||a||^2 \,$ and $ \vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$)
