1

We know that the following property conditional expectation holds, assuming $\mathbb E[|X|]<\infty$:

$\mathbb E\left( {\mathbb E\left( {X|Y} \right)} \right) = \mathbb E(X)$

Could anyone give me some intuition into this? why when we take the expected value again, knowing the random variable Y will not affect the expected value of X.

Math1000
  • 36,983
  • 1
    Are you studying measure theoretical probability or "elementary" probability? – Ian Oct 06 '20 at 12:10
  • 3
    If you want "intuition": assume you want to calculate the average height of puple at school. So first what you can do is just take into account everyone's height. The second way: you can firstly calculate the height of puple in the 1st grade, then in the 2nd, ... and so on, and then take average of their heights. Both calculations should end up the same, – Joitandr Oct 06 '20 at 12:12
  • @Joitandr that makes sense, thanks :) –  Oct 06 '20 at 13:08
  • @lan I don't know either, I am just studying theory of probability. –  Oct 06 '20 at 13:10
  • This is a special case of the "tower rule" - on a probability space $(\Omega, \mathcal F,\mathbb P)$ with sub-$\sigma$-algebras $\mathcal G_1\subset\mathcal G_1\subset F$, if a random variable $X$ defined on $\Omega$ is integrable, then $$ \mathbb E[\mathbb E[X\mid\mathcal G_2]\mid\mathcal G_1] = \mathcal E[X\mid G_1] $$ with probability one. In the special case where $\mathcal G_1={\varnothing,\Omega}$ and $\mathcal G_2=\sigma(Y)$, this reduces to $$ \mathbb E[\mathbb E[X\mid Y]] = \mathbb E[X]. $$ – Math1000 Oct 06 '20 at 16:39
  • I just asked my question above because technically the tower property is baked into the definition of conditional expectation in measure theoretic probability, so there is not really any "analytical" way to prove it in that setting. Instead there is only explaining why the definition does what we want. – Ian Oct 08 '20 at 12:20

2 Answers2

2

The intuition - meaning let's forget about rigor and probability spaces for a second, and just develop a mental cartoon picture of the concept - is actually quite straightforward:

Inside the LHS of the equation $\mathbb E\left( {\mathbb E\left( {X|Y} \right)} \right) = \mathbb E(X)$ we find $\color{blue}{\mathbb E\left( {X|Y} \right)},$ which conditions the expectation of the random variable $X$ on the value of the random variable $Y.$ As such, $ {\mathbb E\left( {X|Y} \right)}$ is actually a random variable, and a function of $Y.$ It is not a number, but a measurable function ${\mathbb E\left( {X|Y} \right)}:Y \to \mathbb R.$ As you slide across the domain of $Y,$ the expectation of $X$ changes, provided they are dependent.

But this expression $\color{blue}{\mathbb E\left( {X|Y} \right)}$ is further enclosed within the operator $ {\mathbb E\left( \cdot \right)},$ which means that we are actually looking for the expectation (weighted mean value) across all values of $Y.$ In doing so, we are essentially integrating, and making the individual values of $Y$ irrelevant.

Pictorially,

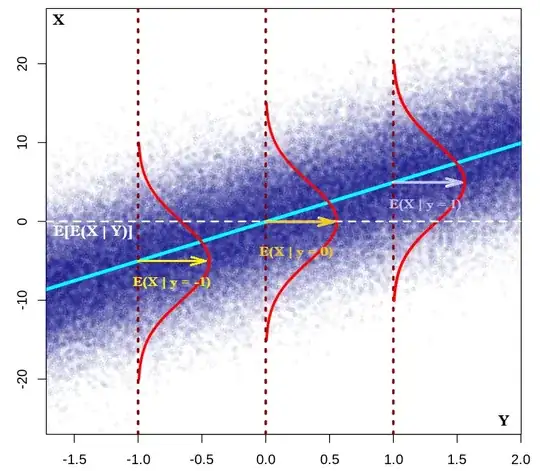
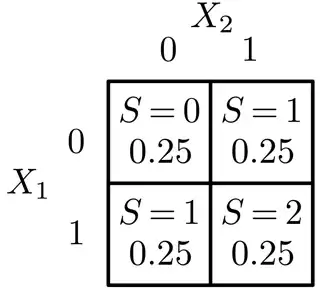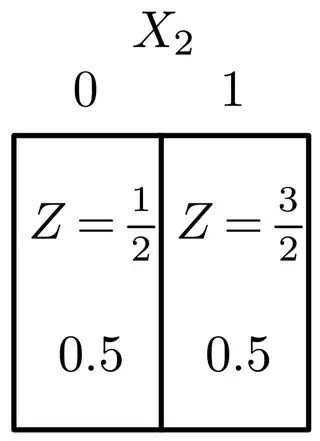enter image description here

Again, just an intuition!

Antoni Parellada
  • 8,889
0

I don't know if these diagrams will be of any use to you. I find it useful to think of conditioning as putting a transparency over the sample space.

Let $X_1, X_2$ be two fair, independent coinflips. Denote the outcome of heads by $0$ and the outcome of tails by $1$. Let $S = X_1 + X_2$. The sample space $\Omega$ has four points: $\{(0,0), (0,1), (1,0), (1,1)\} = \{\omega_1, \omega_2, \omega_3, \omega_4\}$, :

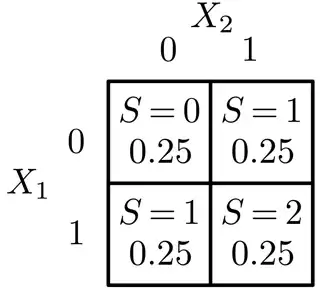
enter image description here

First consider the inner conditional expectation, $Z = E[S | X_2]$. Note that $Z$ is a random variable: for each $\omega \in \Omega$, $Z(\omega)$ is a real number. It's simply that $Z(\omega)$ is constant on the sets $X_2^{-1}(\{0\}) = \{(0,0), (1,0)\} = \{\omega_1, \omega_3\}$ and $X_2^{-1}(\{1\}) = \{(0,1),(1,1)\} = \{\omega_2, \omega_4\}.$ In diagram format,

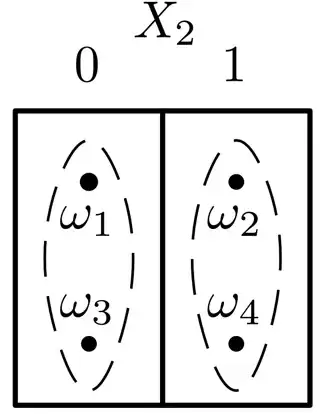
enter image description here

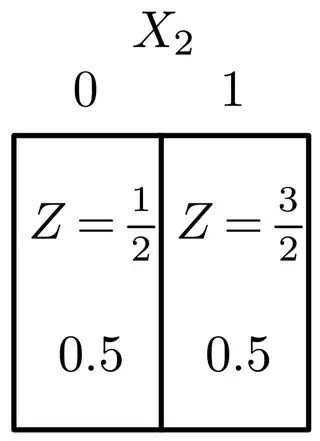
What is the constant value of $Z$ when $X_2 = 0$? It is the conditional probability of $S$ given $X_2 = 0$, which is an average over the $\omega$'s in the set $\{\omega : X_2(\omega) = 0\}$: $$E[S | X_2](\omega_1) = E[S|X_2](\omega_3) = 0.5.$$ Similarly, $$E[S | X_2](\omega_2) = E[S|X_2](\omega_4) = 1.5.$$ enter image description here

Now what happens when you do $E[E[S|X_2]]$? You average again. The rule $E[E[S|X_2]] = E[S]$ can be (roughly) read as "the average of the partial averages is the full average".

snar
  • 7,388
  • 22
  • 25