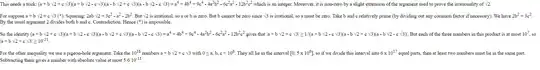1

Show that there are integers $a,b,c$ not all zero, with absolute values less than $10^6$ such that $$|a+\sqrt2 b+\sqrt 3 c|\leq\frac{1+\sqrt2 +\sqrt3}{1+10^6+10^{12}}.$$

I have the read the Putnam Solution for similar question, I don't understand the part that they get the inequality and then apply Pigeonhole theorem there. Link: https://prase.cz/kalva/putnam/psoln/psol804.html enter image description here

HTLL
  • 225
  • 1
  • 7
  • 1
    What have you tried? What are your thoughts on this? – Arthur Oct 05 '20 at 05:37
  • Can we do anything about this expression (a + b √2 + c √3)? Such as finding a, b, c? – HTLL Oct 05 '20 at 05:46
  • Markdown Editing Help: https://math.stackexchange.com/editing-help , How do I ask a good question: https://math.stackexchange.com/help/how-to-ask , MathJax basic tutorial and quick reference: https://math.meta.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference – reyna Oct 05 '20 at 06:32

1 Answers1

1

Let $A = \{ a + b\sqrt{2} + c\sqrt{3} \mid 0 \leq a,b,c \leq 10^6 -1 \}$. Each element of this set lies in the interval $[0,(10^6-1) \times (1+\sqrt{2}+\sqrt{3})]$. Now divide this interval into $10^{18} -1$ consecutive subintervals of length $\frac{(10^6-1) \times (1+\sqrt{2}+\sqrt{3})}{10^{18} -1}$. By the pigeonhole principle, we have that at least two elements of $A$ lie in the same subinterval. So the difference of these numbers is our desired number.

Gary
  • 31,845
Amirhossein
  • 804