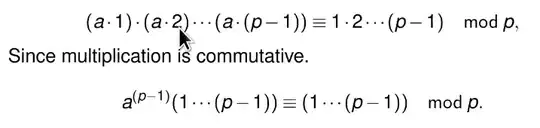This is the start of the proof for FLT:
I was curious -- I know that all the elements of S are unique because gcd(a,p) = 1, but I was wondering -- What would be an example in which the elements were not unique?
Also, in the next step:
what happened to the a? it just disappeared
$x\to ax\,$ is $\,d$-to-$1\,$ mod $\,n,\ d\! =\! \gcd(a,n),\,$ so is $1$-to-$1\!\iff\! \gcd(a,n)\!=\!1\!\iff\! a^{-1}$ exists.
Proof: $\,\ ay\equiv ax\pmod{\!n}\iff n\mid a(y\!-\!x)\iff n/d\mid (a/d)(y\!-\!x)\iff n/d\mid y\!-\!x$
hence $\, y = x + k\,n/d\,$ takes $\,d\,$ distinct values mod $\,n,\,$ viz. for $\,k = 0,1,\ldots,d\!-1.\,$
e.g. for $\,x\mapsto 6x\pmod{\!9}\,$ we have $\,\gcd(6,9)=\color{#c00}{3 = d}\,$ and
$\qquad\qquad\begin{array}{|c|c|} \hline x& \color{#0a0}0 & 1 & 2 & \color{#0a0}3 & 4 & 5 & \color{#0a0}6 & 7 & 8 \\ \hline 6x& \color{#0a0}0 & 6 & 3 & \color{#0a0}0 & 6 & 3 & \color{#0a0}0 & 6 & 3 \\ \hline \end{array}$
is $\,\color{#c00}3$-to-$1\!: $ $\,\{\color{#0a0}{0,3,6}\}\to 0,\ \{2,5,8\}\to 3,\ \{1,4,7\}\to 6$
What happened to the $a$ ? It didn't disappear. The left hand side of the first line has $p-1$ factors of $a$, and they have been consolidated into $a^{p-1}$ in the left hand side of the second line. The right hand side of the first line has simply been copied to the right hand side of the second line.
If you're asking what happened to the $a$ from the left to the right side of the first line, it's because the factors $a \cdot 1, a \cdot 2, \ldots, a \cdot (p-1)$ can be reordered into $1,2,\ldots,p-1$ by the previous step in the proof.
If $n$ is not a prime number, then for any divisor $a$ of $n$ you have $a\cdot\tfrac{n}{a}\equiv0\pmod{n}$. So if $n$ has many factors, you will get many products that are all zero.
For a concrete example take $n=8$ and $a=2$. Then modulo $8$ we have $$S=\{2\cdot1,2\cdot2,2\cdot3,2\cdot4,2\cdot5,2\cdot6,2\cdot7\}=\{0,2,4,6\}.$$
The idea is that multiplication by $a$ yields a permutation of the nonzero residues mod $p$, so $$\{a\cdot1,a\cdot2,\ldots,a\cdot(p-1)\}=\{1,2,\ldots,p-1\}.$$ Then the product of all elements in the LHS is the same as the product of all elements in the RHS: $$1\cdot2\cdots(p-1)=(a\cdot 1)(a\cdot2)\cdots(a\cdot(p-1))=a^{p-1}(1\cdot2\cdots(p-1)).$$
I was curious -- I know that all the elements of S are unique because gcd(a,p) = 1, but I was wondering -- What would be an example in which the elements were not unique?
Well, one where $p$ isn't prime and if $\gcd(a,p) \ne 1$ then you'd have $\frac p{\gcd(a,p)}$ distinct terms and the repeated $a$ times (minus a final term).
Example $a = 3$ and $p=24$ then $a\cdot 1,a\cdot 2, ......, a\cdot (p-1)\equiv 3,6,9,12,15,18,21,0,3,6,9,12,15,18,21,0,3,6,9,12,15,18,21$
what happened to the a? it just disappeared
Not quite
$a, a\cdot 2, a\cdot 3,...., a\cdot (p-1)$ represents a residue system (without $0$) in no particular order. And $1,2,3,......, p-1$ represent a residue system (without $0$). So each $a\cdot j \equiv k_j \pmod p$ for some $0\le k_j \le p-i$.
So $a\cdot a(2)a(3)......a(p-1)\equiv k_1k_2k_3.....k_{p-1}\pmod p$.
And $\{k_1,k_2,k_3,......k_{p-1}\} = \{1,2,3,....,(p-1)\}$ but not in any particular order.
So $k_1k_2k_3.....k_{p-1} = 1\cdot 2\cdot 3.....(p-1)$ because multiplication is commutative and we can put them in numeric order.
Here's an example:
$3^6 \equiv 1 \pmod 7$ because
$S = \{3,6,9,12,15,18\}$ contains a representative of each class $1....,6$. $1\equiv 15;2\equiv 9,3\equiv 3;4\equiv 18;5\equiv 12; 6\equiv 6$.
$3^6\cdot (1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6) =$
$3\cdot 6\cdot 9\cdot 12\cdot 15\cdot 18 \equiv $
$3\cdot 6 \cdot 2\cdot 5\cdot 1\cdot 4 \pmod 7\equiv$ (note those are not in any particular order)
$1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6 \pmod 7$ (but now we just rearranged them into order)
So $3^6(1\cdot ....\cdot 6) \equiv (1\cdot ....\cdot 6)\pmod 7$.
And.... $1\cdot ....\cdot 6$ is relatively prime to $7$ so it is invertible. (Actually be Wilson's Th it is congruent to $-1 \pmod 7$ but ... we don't need to know that.)
$3^6[(1\cdot ....\cdot 6)]((1\cdot ....\cdot 6)^{-1}\equiv (1\cdot ....\cdot 6)(1\cdot ....\cdot 6)^{-1}\pmod 7$ so
So $3^6 \equiv 1\pmod 7$.
