Picture for the Straddle Lemma, in Bartle's Introduction to Real Analysis (2011 4 ed), 6.1.17, p 171?

Question

Can anyone please picture the Saddle Lemma in Introduction To Real Analysis (2011 4 ed) by Robert G. Bartle & Donald R. Sherbert, Section 6.1, Exercise 17, p 171? I'm not asking proofs.

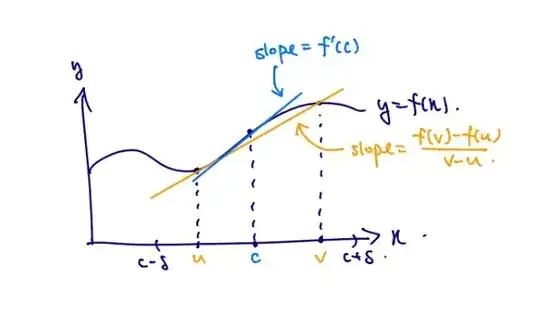
Let $f \colon I \to \mathbb{R}$ be differentiable at $c \in I$. Establish the Straddle Lemma. Give $\varepsilon > 0$ there exists $\delta (\varepsilon) > 0$ such that if $u, v \in I$ satisfy $c-\delta(\varepsilon)<u\leq c \leq v < c+\delta(\varepsilon)$, then we have $\left\lvert f(v) - f(u) - (v-u)f^\prime(c) \right\rvert \leq \varepsilon (v-u)$.
[Hint: The $\delta(\varepsilon)$ is given by Definition 6.1.1. Subtract and add the term $f(c) - c f^\prime(c)$ on the left side and use the Triangle Inequality.]

Answer 1

I'll try to explain it for the case $u\neq v$. The case where $u=v$ yields nothing fruitful.

I believe its geometric interpretation is: at $c$ where $f$ is differentiable, if you confine yourself to a small enough neighborhood of $c$ (which is dependent on $\varepsilon$, your "error tolerance") and pick any two $u$, $v$ in that neighborhood (subject to your conditions of course), the slope of the secant joining the points $(u,f(u))$ and $(v,f(v))$ won't be too different to the slope of tangent at $c$, i.e. the difference is at most $\varepsilon$, your error tolerance.

Here's your picture:

I've exaggerated the size of $\delta$ to make the drawing less cluttered. As you can see, the angle between the blue line (tangent) and the orange line (secant) is quite small, which translate to a small difference in slope. I hope this helps!