2

The three basic angle measurement systems i.e. sexagesimal, centesimal and circular systems are based on a common idea of measuring angles in terms of arc lengths and radii.

Some terminology :

An angle is formed by rotating a "side" about a point. The "side" that is rotated is called the initial side, the point about which it is rotated is called the point of rotation and the side that is obtained after rotating the initial side about the point of rotation is called the terminal side.

Measuring an angle means measuring the extent of rotation made by the initial side to become the terminal side.

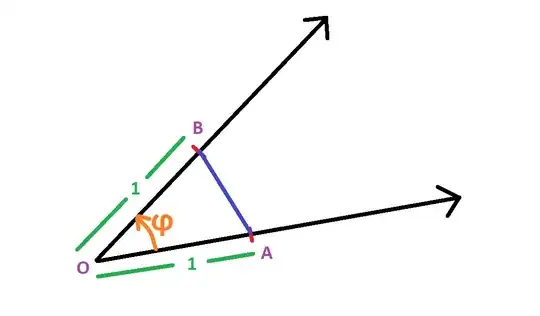
Let's say that in a certain angle measurement system, the unit measure of an angle is equal to the length of the line segment joining two points $A$ and $B$ where $OA = OB = 1~\mathrm{unit}$ ($O$ is the point of rotation) and $A$ and $B$ lie on the initial and terminal sides respectively. For example :

Figure 1

I was wondering if this is a valid way of measuring angles and what its limitations could be.

I think that for an angle measurement system to be valid, it must be true that given the measure of an angle in that system, the angle should be uniquely identifiable and for every angle, the measure of that angle in that system should be unique.

This system would give the measure of all of $60^\circ, 420^\circ, -60^\circ,-420^\circ$ as $1$ but if we constrain this system to $[0^\circ,180^\circ]$ (or $[0,\pi]$), this should not be a problem. In that case, every angle would have a unique measure in this system lying tn the interval $[0,2]$ and for every given measure (in the interval $[0,2]$), the angle would be uniquely identifiable.

Let's denote one unit in this system as $1^a$. So, $1^a = 60^\circ = \dfrac\pi3$ but $2^a \neq 2(60^\circ)$ but rather $2^a = 180^\circ = \pi$. Similarly, $90^\circ = \dfrac 32 \times 60^\circ$ but in this measurement system, $90^\circ = (\sqrt 2)^a \neq \dfrac 32\times 1^a$.

So, unlike degree to radian conversion, where all one needs to do is multiply by a real number (the factor of conversion), the trig functions get involved here.

For an angle $\phi$ whose degree measure is $D$ i.e. $\phi = D^\circ$, the measure of that angle in this new system would be equal to $2\sin\bigg(\dfrac\phi2\bigg)$.

So, how valid is this system of measuring angles? Could it have been the "initial" system for measuring angles, instead of the sexagesimal system?

Thanks!

Rajdeep Sindhu
  • 1,541
  • 1
    What kind of benefits will this system have though? Maybe give an example where this will be useful in? – Lynnx Sep 30 '20 at 05:44
  • @DavidCheng I don't think it has any benefits, though. I'm just doing it is out of curiosity. I want to see how different angle measurement systems work, in what cases one is better than the other etc. – Rajdeep Sindhu Sep 30 '20 at 06:12
  • 1
    This measure $\mu$ is not additive: $\mu(\alpha+\beta)\neq\mu(\alpha)+\mu(\beta)$.. – gpassante Sep 30 '20 at 06:19
  • @RajdeepSindhu But when we are defining something, most of the time we do so because it has some nice properties we want. And being additive is a super nice properties that we want. It makes sense to introduce a definition when it can simplify things a lot, for example, in relativity, we define Rapidity instead of using velocity, so that it has the nice property of being additive and such. – Lynnx Sep 30 '20 at 06:26
  • @gpassante That's a great point. – Rajdeep Sindhu Sep 30 '20 at 06:27
  • I think it could have been! Prof Norman Wildberger has written a book on Rational Trigonometry (https://en.wikipedia.org/wiki/Rational_trigonometry) in which he proposes using "spread" to measure angles (on a scale of 0 to 1). His system, like yours, is simpler in some respects but not as nice in others (i.e. has advantages/disadvantages). – Selrach Dunbar Sep 30 '20 at 06:28
  • @gpassante $\mu(\alpha)$ is the function that converts $\alpha$ to this measure system right? i.e. $\mu(\alpha) = 2\sin(\alpha/2)$. Here : $$\mu(\alpha+\beta) = \dfrac{\mu(\alpha)\sqrt{4-\mu^2(\beta)}+\mu(\beta)\sqrt{4-\mu^2(\alpha)}}{2}$$ – Rajdeep Sindhu Sep 30 '20 at 06:46
  • @Rajdeep Sindhu Nice. Very far from additivity! – gpassante Sep 30 '20 at 07:22
  • @gpassante ${}$ – Rajdeep Sindhu Sep 30 '20 at 07:32

0 Answers0