5

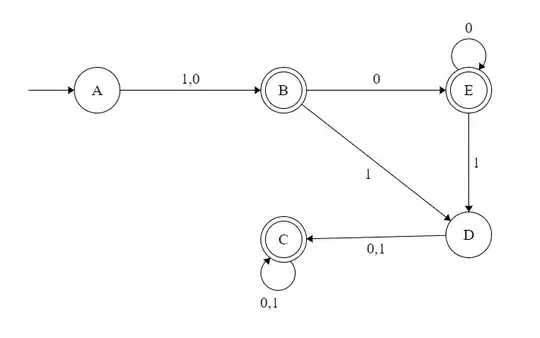
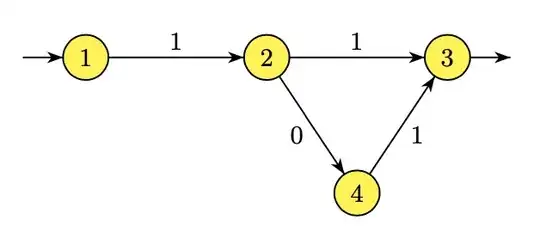
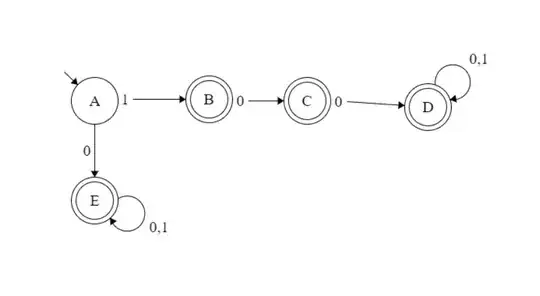
I would like to verify if i have the good approach to this problem, while looking at my solution it seems ok but i am not sure. Thank you.

I am using this tool to draw if you wanna help out : http://madebyevan.com/fsm/

Here's the question :

Build a finite automata ( it can be deterministic or not) that accept this language on the alphabet $\{0,1\}$ :

$$L=\{w : w \neq 11 \text{ and } w \neq 101 \}$$

In other words, L includes all sequences except 11 and 101

Here's what i tried :

enter image description here

Wolgwang
  • 1,563
codetime
  • 335
  • 2
  • 8
  • 1
    I think you mean "$\neq$", which is "$\neq$". – Eric Towers Sep 28 '20 at 23:41
  • 1
    What does your automaton do with input "$1001$"? – Eric Towers Sep 28 '20 at 23:43
  • @EricTowers err, good point would i need a new link from E to C with a 0 ? – codetime Sep 28 '20 at 23:47
  • Your automaton does the same thing whether the string starts with $o$ or $1$. This can't be right, since it accepts all strings that start with $0$, but rejects some that start with $1$. Also, the initial state should be an accepting state, because the empty string is in the language. – saulspatz Sep 29 '20 at 00:08
  • @saulspatz Thanks for reply, i am not sure why can't it do the same things wether it starts with 0 or 1, the only restriction is that it cannot be 11 or 101. The first link is for sure 0 or 1, im not sure why i can't start like that ? Thanks. – codetime Sep 29 '20 at 01:37
  • If I understand you correctly, you want to reject $11$ but accept $01$. If you go to the same state, whether you get a $0$ or a $1$, and then you get a $1$, what do you do? – saulspatz Sep 29 '20 at 03:38
  • @saulspatz yes every words are accepted except 11 and 101, this is why at the start i said : From A with a 1 or 0 u can go to B and it's accepted but if you get a 1 u go to D which is not an acceptation state, can i just remove the link from B to D here ? i am confused – codetime Sep 29 '20 at 03:42
  • No. You cannot go from A to B on both $0$ and $1$. If the machine is in state B, it doesn't know how it got there. There is no way for it to know that it should accept $01$ but reject $11$. – saulspatz Sep 29 '20 at 03:50
  • I bookmarked this question just for the link to the drawing tool. Thanks. – user400188 Sep 29 '20 at 09:04

4 Answers4

0

You might benefit from constructing a complete binary tree of depth three (each internal node has one child consuming a "0" and one consuming a "1"), determining which nodes are rejecting, which are accepting, and then simplify the tree.

Eric Towers
  • 67,037
0

Your DFA fails to accept the string $1001$. It would be better if you draw a DFA for $L=\{11,101\}$ and then take the compliment.

Beyond Infinity
  • 164
0

Your detailed question deserves a detailed answer. It is indeed easier to take the complement of the language, that is, $L^c = \{11, 101\}$, and first compute its minimal automaton. Note that the method suggested by Eric Towers would give a deterministic automaton, but not the minimal one. The minimal deterministic incomplete automaton of $L^c$ is represented below

$\hskip 100pt$

Now, to get the minimal deterministic automaton of $L$, just add the sink state $0$ and swap the final states.

$\hskip 100pt$

P.S. As you indicated your source to draw automata, here is mine. These automata were obtained using the $\LaTeX$ package gastex.

J.-E. Pin
  • 40,163
  • Thanks for reply, in the second graph i am not sure what the arrows going out at 1 , 2, 4 and 0 with nothing on it means, i've never seen that ? Thanks. – codetime Sep 29 '20 at 13:31
  • This is just another notation for the final states. Intuitively, it means that you can leave when you arrive to this state. – J.-E. Pin Sep 29 '20 at 13:57
  • @Je.-E. Pin oh right, also is it better to have a graph like Donald Splutterwit did ? Or should i conserve the link that does 1 1 and 101 with a non-accepting state ? Or both are valid ? Thanks again. – codetime Sep 29 '20 at 16:30
  • 1
    @codetime Sorry to say, but Donald Splutterwit's answer is plain wrong. – J.-E. Pin Sep 29 '20 at 17:58
  • good point, i read it fast, thank you and thanks for the tip on how to figure it out. I'll let this post until tonight and then choose this as the answer thanks :) – codetime Sep 29 '20 at 18:13
  • You're welcome. – J.-E. Pin Sep 29 '20 at 18:55
-1

We want to avoid $11$ and $101$ enter image description here

Donald Splutterwit
  • 36,613
  • 2
  • 26
  • 73
  • Does the graph from J.-E. Pin also works, but the state is not accepting when u reach 11 ( from 2 he can go to 3 with a 1 and the state 3 doesnt accept). Both works right (yours and his) ? Thank you. – codetime Sep 29 '20 at 16:16
  • 1
    $110$ is not accepted, but it should be. – J.-E. Pin Sep 29 '20 at 17:55