How many ways are there to arrange the letters $A$, $A$, $B$, $B$ around a circle?
My first go with was is to arrange $4$ objects around a circle with gets us $(4-1)!$ but we have to take care of the inner arrangements of $A$, $A$ and $B$, $B$ which leaves us with $$\frac 6 {2! \cdot 2!} $$ but that's obviously wrong. I have tried other methods too but they fail to generalize.
By counting by hand for both the $2A$'s and $B$'s case and the $3A$'s and $3B$'s case we get the answers $2$ and $4$ respectively (hopefully I didn't make any mistakes counting)
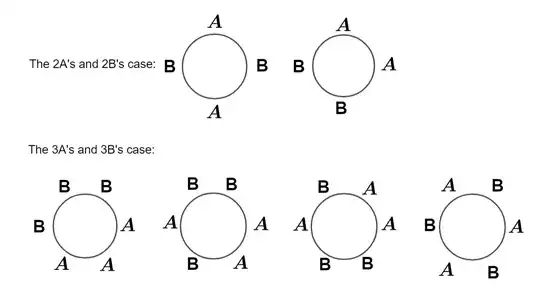
- what's wrong with my argument?
- what's the right method for solving this?
- how can this be generalized?