7

There isn't much background context, but is there any estimations on how many iterations of $n \to p\% n$ are needed before $n$ becomes 0? Percentage sign is modulo. ($p$ is fixed, prime in my context but not sure if it matters).

For example, when $p=10^9+7$, the maximum number of iterations needed is $50$. When $p=998244353$ (a common prime in competitive programming) the number of iterations is $45$. I don't see any proof that it requires approximately $\log p$, but it seems like so.

Thank you for your time and help.

Gareth Ma
  • 1,853
  • Also just to add, there probably isn't a closed form? So some approximate would be enough (upper bound or sth) – Gareth Ma Sep 27 '20 at 15:25
  • What is the start value of $n$ ? – Peter Sep 27 '20 at 15:27
  • 2
    @Peter Any value between 0-(p-1), and I want the maximum number of iterations. (if n>p it will end in two steps right haha) – Gareth Ma Sep 27 '20 at 15:28
  • 1
    This is close to but not quite an algorithm for computing the continued fraction expansion of $\frac{p}{a}$ (where $a$ is the initial value); the continued fraction computation ends after something like $\log_{\phi}(p \sqrt{5})$ steps which roughly matches up with the numbers you gave, but it doesn't actually quite match up to the continued fraction algorithm unfortunately. – Qiaochu Yuan Sep 27 '20 at 19:05
  • Ah I see, as we can think of continued fraction as $(a,b)\to (b,a% b)$, whereas here is $(a,b)\to (a,a% b)$.(?) I'll try and see if that helps – Gareth Ma Sep 27 '20 at 23:28
  • 1
    Why is 998244353 a common prime in competitive programming? I mean, it’s close to a power of 10, but not that close- surely there are primes closer to $10^9$. – Lieutenant Zipp Sep 28 '20 at 05:08
  • 1
    @LieutenantZipp 119x2^24+1 useful for numeric theoretical transformation (NTT) – Gareth Ma Sep 28 '20 at 05:09
  • 1
    @Qiaochu Actually it's the descent step of Gauss's algorithm for computing modular inferences. – Bill Dubuque Sep 28 '20 at 08:22
  • @BillDubuque this question actually comes from a recursive relation to find a modulo inverse, which is what your links algorithm describes. Is there any upper bound on number of iterations before it ends? – Gareth Ma Sep 28 '20 at 08:30
  • Hint: If you used a least magnitude residue system then each step decreases $n$ by at least a factor of $2\ \ $ – Bill Dubuque Sep 28 '20 at 08:34
  • @GarethMa Are you interested in the worst case (an upper bound that holds always) or the average case (the approximate value) ? – Peter Sep 28 '20 at 09:04
  • @Peter Both are fine and interesting for my purpose. Also, this is the source of the discussion (quite a lot of code): https://codeforces.com/blog/entry/83075 – Gareth Ma Sep 28 '20 at 09:33
  • @GarethMa If you want, I can write a pari/gp-routine, but I have no idea for an efficient approach, it will take long for large $p$. – Peter Sep 28 '20 at 09:35
  • 1
    If you use a least magnitude residue system as @BillDubuque suggested, then you easily get an $O(\log p)$ bound. But if you're using a least nonegative residue system, the algorithm generally takes more steps ($p = 419$ gives e.g. $7 \to 6\to 5\to 4 \to 3 \to 2 \to 1 \to 0$ against $7 \to -1 \to 0$). I still expect an $O(\log p)$ bound, but I don't (yet?) see how to prove it. – Daniel Fischer Sep 28 '20 at 10:52
  • @DanielFischer Precisely what do you mean by "generally" above? – Bill Dubuque Sep 28 '20 at 17:26
  • @BillDubuque That there are many pairs $(n,p)$ for which the number of iterations needed to reach $0$ is larger when $p \mathbin{%} n$ denotes the least nonnegative residue than if it denotes the least magnitude residue. Not "generally" as in "always". – Daniel Fischer Sep 28 '20 at 17:33
  • @DanielFischer what does the arrow mean ? "Approaches", right ? – Spectre Dec 02 '20 at 17:00
  • @Spectre No, it means one iteration. So for example say p=13 and $n$ starts at 5, then it'll go like $n=5 \to 13%5=3 \to 13%3=1 \to 13%1=0$ – Gareth Ma Dec 02 '20 at 17:01
  • @DanielFischer oh... so $n$ is updated every time... Thanks ! – Spectre Dec 02 '20 at 17:02
  • @GarethMa is $p$ prime ? – Spectre Dec 03 '20 at 05:14
  • @Spectre for my purpose, yes. – Gareth Ma Dec 03 '20 at 05:15
  • @GarethMa I have put up a post here regarding it, but I didn't assume that it is prime, so as to look at the problem from a wider view. – Spectre Dec 03 '20 at 05:17
  • @GarethMa, and is $n$ random ? – Spectre Dec 03 '20 at 05:19
  • No restrictions than $0 < n < (p - 1)$, right ? – Spectre Dec 03 '20 at 05:19
  • @Spectre yes. I am mainly interested in average and worst case performance (=number of iterations) for all input of n, but any progress would be great – Gareth Ma Dec 03 '20 at 05:20
  • @GarethMa thanks for the details.. – Spectre Dec 03 '20 at 05:22
  • @GarethMa a beautiful solution has arrived ! – Spectre Dec 03 '20 at 12:15

2 Answers2

2

Let us remove the constraint that $p$ is a prime number. Given a strictly decreasing sequence $1=a_0 < a_1 < \ldots < a_k$ and consider the set

$$ S(\textbf{a}) := \{p: p \equiv a_j \pmod{a_{j+1}} \ \ \forall j = 0 \ldots k-1\} $$

This is exactly the set of numbers that will produce the sequence $\textbf{a}$ during this process. Note that this set is stable for shifting by $\text{lcm }\{ a_1, \ldots, a_k\}$, and that the set of solutions is determined by applying the chinese remainder theorem.

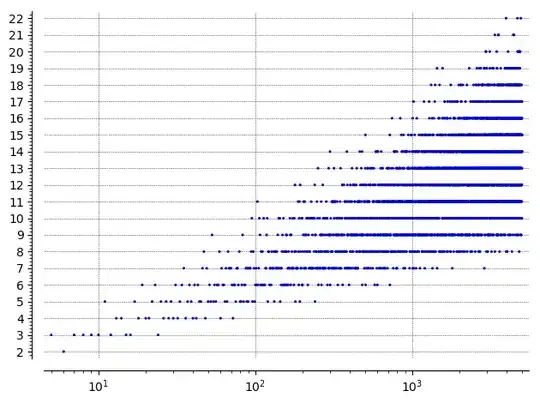
We will consider two particular sequences to get the following result: (1) there exist arbitrarily large (prime) numbers that ends in $2$ iterations; (2) there exist arbitrarily large numbers that ends in at least (about) $(\log p) /2 $ iterations.

For the first just consider the sequence $3>1$ and take a (prime) number $p\equiv 1 \pmod{3}$.

The second is more interesting. Consider the sequence $k > \ldots > 1$. This means that we have $p$ such that $p\equiv m-1 \equiv -1 \pmod{m}$ for all $m\le k$. Solutions of this system are exactly numbers that are $\equiv -1$ modulo $L_k:= \text{lcm}\{1, \ldots, k\}$. The smallest such positive number is exactly $L_k -1$. We can give an estimate of $\log L_k$ as starting from the equation

$$ L_k = \prod_{p \le k} p^{[\log k/\log p]}$$

Indeed, any prime will appear with the maximum exponent it can appear with. Taking the logarithm we get

$$ \log L_k = \sum_{p\le k} (\log p) [\log_p k] \le \sum_{p \le k} (\log p) (\log_p k +1) $$ $$ = \sum_{p\le k} \log k + \log p \le \sum_{p\le k} 2 \log k \approx (2 \log k) \frac{k}{\log k} = 2k $$

Using the prime counting theorem $|\{p\le k\}| \approx k/\log k$. Recall that $k$ is the number of iterations relative to the input number $p=L_k-1$. Thus we get $$( \log p )/2 \approx ( \log L_k)/2 < k$$

Giving the desired solution.

Andrea Marino
  • 5,384
  • 1
    Nice work, sir ! (+1) – Spectre Dec 03 '20 at 12:14
  • 1
    Sorry for the late reply, I didn't check the site. Thank you for your solution, I might need a bit more time to sit down and work through it, but thank you for your effort! I will accept hopefully soon, when I understand it <3 – Gareth Ma Dec 05 '20 at 09:11
  • Thank you! Feel free to ask if you need clarifications :) – Andrea Marino Dec 05 '20 at 12:03
  • I reviewed the calculations and I was wrong in some details. Fortunately, this resulted in a better estimate :) I think now it should be easier to read – Andrea Marino Dec 05 '20 at 12:38
0

Here's a semi-logarithmic plot of the maximum number of iterations required for a given $p$, with $p$ ranging from 5 to 5000, checking all $2 \le n < p-1$. Both the best & worst cases do seem to be growing logarithmically.

max iterations plot

And here's a plot of the mean number of iterations, for $1 \le n < p$.

mean iterations plot

These plots were produced using Sage / Python. You can play with an online interactive version here (the script is actually encoded in the URL, not stored on the server). If you set the 'hi' parameter too high, the server will probably time out.

PM 2Ring
  • 4,844