Deriving $\cos(a+b)$

Question

I was able to derive $\sin(a+b)$ using a geometric construction of two terminal rays where the long 1 has a hypotenuse of 1. The right triangle with hypotenuse 1 formed by angle $b$ is the triangle $\triangle ADC$, the other right triangle formed by angle $a$ is $\triangle ACB$. 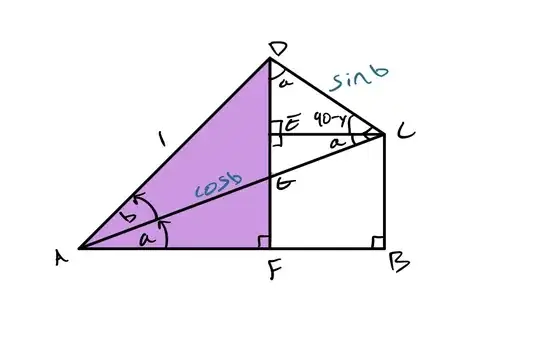I saw that $\overline{CB}=\sin a \cos b$ and $\overline{DE}=\cos a \sin b$. Likewise I notice that $\cos(a+b)=\overline{AF}$. But I'm having no success using what I know about the double angle of sine to derive the formula for the double angle of cosine. I tried using similar triangles and the farthest that got me is that $\overline{AB}=\sin a \cos^2 b$