What exactly do systems of equations represent?

Question

Systems of equations are taught pretty early in American curriculum. We are taught methods of substitution and methods of elimination in order to solve them. We are taught how to use matrices or graphs as alternative strategies to encode/visualize them.

There are linear systems of equations...there are non-linear systems of equations...and there are systems of equations with 1 or many variables. However, to this day, I still do not really understand what systems of equations are. I've tried to find an abstract interpretation of systems of equations but without much success. I am very interested in figuring out this "systems of equations abstraction" because there are canonical statements (e.g. the classic "You need as many equations as variables to find a solution") that I would very much like to prove.

I've tried myself to come up with some semblance of an abstraction but I have not made much progress. I will illustrate the case for one equation with one variable and two equations with two variables (which is where I run in to trouble).

One Equation - One Variable

Consider the purely arbitrary equation: $$a = b +\alpha x \ \text{ where}\ \alpha \neq 0$$

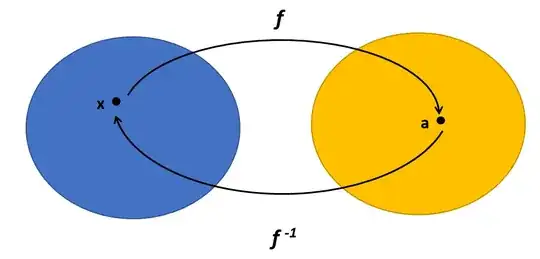
The effort to solve this equation can be rephrased as "Find me the $x$ that maps to $a$ through the function $f(x) = b + \alpha x$." In effect, therefore, this question is one requiring that we find the inverse function $f^{-1}$ that, when $a$ is given as input, $x$ will be output.

Solving for $x$ by virtue of substracting $b$ from both sides and dividing both sides by $\alpha$ effectively amounts to determining the inverse function such that: $f^{-1}(x')=\frac{x' -b}{\alpha}$...for future purposes, also note that this can be denoted as $f^{-1}\big(f(x)\big)=\frac{f(x) -b}{\alpha}$ . Plugging in $a$ for $x'$ we arrive at the solution to this equation, which is $f^{-1}(a)=\frac{a-b}{\alpha}$. So far, so good.

Two Equations - Two Variables

Consider the following two arbitrary equations of two variables:

$$a=b+\alpha x + \beta y \ \text{ where}\ \alpha, \beta \neq 0$$

$$c=d +\gamma x + \delta y \ \text{ where}\ \gamma, \delta\neq 0$$

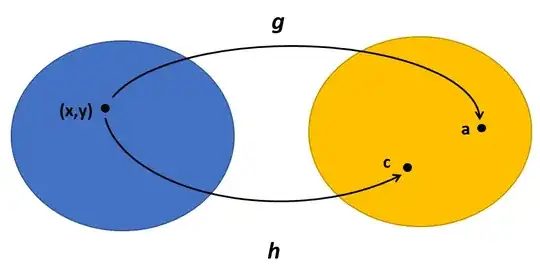
Following the same logic of the "One Equation - One Variable" section, solving for $x$ and $y$ can be viewed as constructing the inverse functions for the two above equations, which can be recast as specific instances of:

$$g\big( (x,y) \big) = b+\alpha x + \beta y$$

$$h \big ( (x,y) \big ) = d +\gamma x + \delta y$$

As to how one solves for these inverses, I have not the faintest clue. Obviously, we could revert to the standard methods of substitution and arrive at the following bulky solutions:

$$ y = \frac{\alpha \Big ( h \big((x,y)\big) -d \Big) -\gamma g\big( (x,y) \big)+\gamma b}{\delta \alpha - \beta \gamma}$$

and

$$ x = \frac{g\big( (x,y) \big) -b - \beta y}{\alpha}$$

However, these are not inverses of the functions $g$ and $h$. In fact...I don't really even know WHAT these equations represent. If you were to plug in the value of $y$ in the final equation for $x$ (I omitted that for brevity), you can see that the $y$ equation and the $x$ equation both have $g\big ( (x,y) \big)$ and $h \big ( (x,y) \big)$ in them...so these equations are inverse-like. That is to say, determining $(x,y)$ requires information from both $g$ and $h$, which provides the first clues as to how one might prove, "You need as many equations as variables to find a solution." Linking this back to the "One Equation - One Variable" section, recall that $f^{-1}\big(f(x)\big)=x = \frac{f(x)-b}{\alpha}$ depends on only one function in order to solve.

Hopefully I did not completely botch this question and was able to sufficiently convey what I am after. Any insights would be greatly appreciated. Cheers~

Answer 1

Bringing in the language of inverse functions and so on isn't unreasonable, but in my opinion makes things more mysterious than they need to be. Instead I prefer a more set-theoretic, or perhaps "generalized geometric," interpretation.

The basic idea is that equations carve out geometric shapes in the relevant space, e.g. $\mathbb{R}^3$ - namely, their solution sets. Similarly, systems of equations then correspond to intersections: a system of equations describes the intersection of the shapes described by the individual equations in it. Algebraic forms correspond to geometric properties and vice versa, and this often lets us relate geometric and algebraic results: e.g. consider "three 'general' linear equations in three unknowns have a unique solution" versus "three planes in $\mathbb{R}^3$ in 'general position' have a single point in common."

Solving an equation, or system of equations then amounts to giving a "simpler" description of the corresponding set (and in particular, this simpler description should make it clear whether that set is nonempty). Note that this means that the solution process is "just" rephrasing. One slogan I like in this context is the following:

The equation becomes the answer.

The various tools we're "allowed" to use in solving a (system of) equation(s) correspond to theorems relating the solution sets given by certain related (systems of) equations, especially those which show that two equations have the same solution set:

• The fact that e.g. adding something to both sides of an equation doesn't affect the solution set is a consequence of the basic rules of equality in first-order logic.

• Other techniques are more context-specific: e.g. the fact that we can add "$a-a$" to one side of any equation relies on the particular axioms governing subtraction.

• As a more complicated example, by the field axioms the solution set of $s=t$ is the union of the solution set of the equation ${s\over x}={t\over x}$ and the solution set of the system of equations $\{s=t, x=0\}$. Here we're not just asserting an equality between two solution sets, it's more complicated than that (and explains why division "feels different" as an equation-solving tool).

But "(systems of) equations are sets" is not the end of the story! There is in fact a second slogan which pushes us in a new direction:

Equations have lives of their own.

For example, we can consider "$4x^2-3y=17$" over $\mathbb{R}$, or over $\mathbb{C}$, or over $\mathbb{H}$, or over the integers modulo $42$, or etc.. Changing the structure changes the set associated to the equation, often leaving the realm of what we naively consider "geometry" altogether. The subject of algebraic geometry involves broadening our perspective on what constitutes "geometry" to include such things, though, and this broadening has turned out to be extremely useful.

In summary:

Equations, and systems of equations, describe ways of assigning sets, which we may try to think of as being shapes in some sense, to structures. Solving them (over a given structure) amounts to giving a nice description of the corresponding set.

And looking ahead to logic (everybody loves logic, right? :P), by generalizing this idea substantially at the cost of largely losing the geometric flavor we wind up with model theory - see e.g. here.

Answer 2

To understand what a system of equations is, you need to, I'd say, understand better what an equation, itself, is, and that requires you to even go back a step further and understand the notion of what an expression is, and its evaluation.

An "expression" is a "grammatically correct" set of mathematical symbols, that stands in for, and thus specifies, a particular mathematical object, such as a number, set, or matrix, and the process of determining which object an expression refers to is called evaluation of that expression. For example, the expression "$5 + 9$" (for the usual definition of "5", "9", and "+") refers and evaluates to the number "14". The expression $9 - 5$, likewise, refers to the number "4". Note that "$14$" and "$4$" are even themselves expressions; it's just that their evaluations are trivial.

An equation, then, is an example of a special type of expression called a Boolean expression, also called a "predicate". Unlike the above expressions which evaluate to numbers, Boolean expressions evaluate to a logical value, i.e. either "True" or "False" in the system of logic most commonly employed in mathematics. In this framework, the "$=$" in the equation is actually, itself, a function, just like $+$, that also, just like $+$, takes two arguments (so it's a "binary function"), but which returns, instead of a number, a logical value. For example, "$5 = 5$" evaluates to "True", but "$5 = 9$" evaluates to "False". Semantically, "$a = b$" means "$a$ is identical to $b$", so the Boolean function $=$ gives "True" only when both its input arguments are the same thing, otherwise it gives "False".

Then, when we say "such that $\mbox{(smth 1)} = \mbox{(smth 2)}$" or the like in English, we are saying "such that the Boolean expression '$\mbox{(smth 1)} = \mbox{(smth 2)}$' evaluates to 'True'".

That's what a single equation is.

So what's a system of equations? Well, it's again another Boolean expression, i.e. logic-valued thingy, only we now join them together with "ANDs". That is,

$$\begin{cases}\mbox{(expr 1)} = a_1\\ \mbox{(expr 2)} = a_2\\ \cdots\\ \mbox{(expr $n$}) = a_n\end{cases}$$

is just another notational flourish for the Boolean expression or predicate

$$[\mbox{(expr 1)} = a_1] \wedge [\mbox{(expr 2)} = a_2] \wedge \cdots \wedge [\mbox{(expr $n$)} = a_n]$$

where $\wedge$ now is another binary Boolean function representing "and" which, as you may or may not expect, is "True" only when both Boolean inputs into it are also "True".

Finally, the notion of "solving" an equation or equation system just means "find me the values I should plug into the variables to make the Boolean expression it stands for evaluate to 'True'".

The other answer here mentions sets - in fact, these two things are very closely connected, because sets and Boolean expressions (predicates) mirror each other in a very simple way: we can represent any Boolean expression by its solution set, i.e. the set of all assignments of the variables which make it evaluate to "True" - or better, as a Boolean expression involving set membership $\in$, i.e.

$$(x_1, x_2, \cdots, x_n) \in S$$

for some set $S$ of combinations of values of the variables. However, sets are much more general in that the converse of this fails: an arbitrary set has no guarantee at all to be expressible as a Boolean expression, whether an equation, system of equations, or otherwise, involving only simple functions like $+$ and predicates like $=$, amongst its variables. Most sets, in fact, can only be represented by meticulously writing down all their members, which may be infinite: even very, very infinite.

Indeed, one can say the whole purpose of sets is to make this "converse" fail: they are to give us access to, and reason about, a much broader, more universal notion of predicate beyond just the ones we can write down explicitly. "A set describes a property of its members", is one way to put this, and this is also why that sets do not admit repeated members, which may not be so obvious from the way they are typically introduced as "bags of stuff".

Answer 3

A system of equations can be understood as a set of equalities over a given FOL structure. It is the structure that tells you what operations are allowed, which allows you to form terms possibly with free variables, and each equality is simply a formula of the form "$t=u$" where $t,u$ are terms over the structure. You have to understand FOL in order to fully understand what equations mean.

For example, polynomial equations over a ring are simply equalities over that ring. When you solve a system of linear equations with real coefficients, what you are essentially doing is finding a tuple of reals that can be assigned as values to the free variables of those equations to make them true in the structure of reals. More generally, Gaussian elimination on a linear system of equations works over any field, not just the field of reals, because all the operations you use in Gaussian elimination are supported by any such field.

This viewpoint readily captures the most general notion of "equation system" that you are likely to encounter in practice. For example, you can have a system of differential equations as well, where the underlying structure is often a 2-sorted structure $((ℂ,F),D,...)$, where the first sort $ℂ$ is the complex numbers, and the second sort $F$ is the set of differentiable functions on some subset of $ℂ$, and $D$ is the differentiation operation on $F$, and the "$...$" are for all the usual operations that come with $ℂ$ and $F$. For example, the system $\Big\{ \frac{dx}{dt} = a·y , \frac{dy}{dt} = b·x \Big\}$ where $a,b∈ℂ$ would formally be the system $\{ \ D(f) = scale(a,g) \ , \ D(g) = scale(b,f) \ \}$ where $scale : ℂ×F→F$ is the operation representing the scalar multiplication of a complex number on a function in $F$, and $f,g$ are free variables of sort $F$.

By the way, you do not need as many equations as variables to find a solution. $\{ x+y = 0 \}$ has one equation but two variables, yet you can easily find a solution... What you probably wanted to say was "unique solution", which applies to linear systems of equations over a field and not in general. For instance, $\{ x^2+y^2 = 0 \}$ has one equation but two variables, and yet has a unique solution over the reals.

Also, as you might realize by now, the fact that solution sets for linear systems of equations over a field forms a hyperplane is quite a special one, and the general situation is much messier. Just for example, $\{ x+y = 2 , x-y = 1 \}$ has no solution over the integers.