Complex analysis integral residuum

Question

I am asked to evaluate, principal value of $$\int_{-\infty}^\infty\frac{\cos(x)}{a^2-x^2} \, dx=\pi \frac{\sin (a)}{a},a>0$$

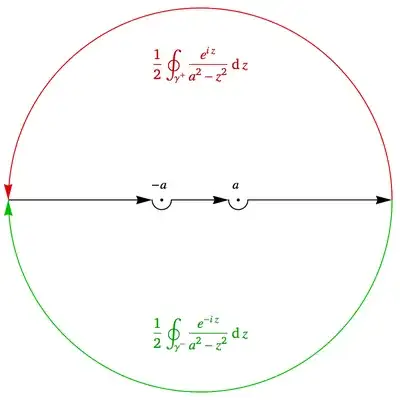
If we start from $$\oint\limits_{C}\frac{e^{iz}}{a^2-z^2}dz,a>0$$ the line $C$ is composed of the half circle $\Gamma$, pole circles at $-a,a, \gamma_1,\gamma_2$ whose circumferences are ($r,r_1,r_2$), and a portion of the $x$-axis. If we use the Cauchy remainder theorem, we get $$ \begin{split} \int_0^\pi \frac{e^{ir\cos \theta -r\sin \theta}} {a^2-r^2e^{2-\theta}} ire^{i\theta} \, d\theta &+ \int_{-r}^{-a-r_2} f(x) \, dx + J_2 \\ &+ \int_{-a+r_2}^{a-r_1} f(x) \, dx + J_1 + \int_{a+r_1}^r f(x) \, dx = 0 \end{split} $$ Since $\left|\int_0^\pi \frac{e^{ir\cos \theta -rsin \theta}}{a^2-r^2 e^{2-\theta}}ire^{i\theta} \, d\theta\right|\leq{\frac{\pi r}{r^2-a^2},(r>a)}$ We get $$\lim_{n \to \infty}\int_0^\pi \frac{e^{ir\cos \theta -r\sin \theta}}{a^2-r^2e^{2-\theta}}ire^{i\theta} \, d\theta=0$$ Evaluating residuum at $J_{1}$ and $J_{2}$ we get $$J_1=\operatorname{Res}f(a)=\lim_{x \to a}(a-x)\frac{e^{ix}}{(a-x)(a+x)} =\frac{e^{ia}}{2a}$$ and $$J_2= \operatorname{Res}f(-a)=\lim_{x \to -a}(a+x)\frac{e^{ix}}{(a-x)(a+x)}=\frac{e^{-ia}}{2a}$$ In my book the author got $J_{1}=\frac{\pi i}{2a}e^{ia}\land J_2=-\frac{\pi i}{2a} e^{-ia}$ Where does the $\pi i$ come from ? also, why - in the second one? Is it because the residuum is at $-a$? Then, adding those two gives us the result, but still, where does $\pi$ come from?

Answer 1

I suspect that the author meant to write $\pi i$ times the residue terms. And the residue at $z=a$ is given by

$$\lim_{z\to a}(z-a)\frac{e^{iz}}{a^2-z^2}=-\frac{e^{ia}}{2a}$$

---

So, in order to provide support of your analysis, let's start from scratch and evaluate the closed contour integral

$$\begin{align} 0&=\oint_C\frac{e^{iz}}{a^2-z^2}\,dz\\\\ &=\int_{-R}^{-a-r}\frac{e^{ix}}{a^2-x^2}\,dx+\int_\pi^0 \frac{e^{i(-a+re^{i\phi})}}{a^2-(-a+re^{i\phi})^2}\,ire^{i\phi}\,d\phi\\\\ &+\int_{-a+r}^{a-r}\frac{e^{ix}}{a^2-x^2}\,dx+\int_\pi^0 \frac{e^{i(a+re^{i\phi})}}{a^2-(a+re^{i\phi})^2}\,ire^{i\phi}\,d\phi\\\\ &+\int_{a+r}^R \frac{e^{ix}}{a^2-x^2}\,dx+\int_0^\pi \frac{e^{iRe^{i\phi}}}{a^2-(Re^{i\phi})^2}\,iRe^{i\phi}\,d\phi\tag1 \end{align}$$

The last integral on the right-hand side of $(1)$ vanishes as $R\to\infty$. And as $r\to 0^+$, the second and fourth integrals on the right-hand side of $(1)$ approach $-\frac{i\pi e^{-ia}}{2a}$ and $\frac{i\pi e^{ia}}{2a}$, respectively.

We find, therefore, that the Cauchy Principal Value of the integral of interest is

$$\begin{align} \text{PV}\left(\int_{-\infty}^\infty \frac{\cos(x)}{a^2-x^2}\,dx\right)&=\lim_{r\to 0^+}\left(\int_{-\infty}^{-a-r}\frac{\sin(x)}{a^2-x^2}\,dx+\int_{-a+r}^{a-r}\frac{\sin(x)}{a^2-x^2}\,dx\\\\ +\int_{a+r}^\infty\frac{\sin(x)}{a^2-x^2}\,dx\right)\\\\ &=\frac{\pi\sin(a)}{a} \end{align}$$

as was to be shown.

Answer 2

$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ $\ds{\large\mbox{An}\ alternative:}$

---

With $\ds{\Lambda > \verts{a}}$: \begin{align} &\bbox[5px,#ffd]{\mrm{P.V.} \int_{-\Lambda}^{\Lambda}{\cos\pars{x} \over a^{2} - x^{2}}\,\dd x} \\[5mm] = &\ {1 \over 2\verts{a}}\,\mrm{P.V.}\int_{-\Lambda}^{\Lambda}{\cos\pars{x} \over x + \verts{a}}\,\dd x - {1 \over 2\verts{a}}\,\mrm{P.V.}\int_{-\Lambda}^{\Lambda}{\cos\pars{x} \over x - \verts{a}}\,\dd x \\[5mm] = &\ {1 \over 2\verts{a}}\,\mrm{P.V.}\int_{-\Lambda + \verts{a}}^{\Lambda + \verts{a}} {\cos\pars{x - \verts{a}} \over x}\,\dd x + \pars{~\verts{a} \mapsto -\verts{a}~} \\[5mm] = &\ {1 \over 2\verts{a}}\,\mrm{P.V.}\int_{-\Lambda + \verts{a}}^{\Lambda - \verts{a}} {\cos\pars{x - \verts{a}} \over x}\,\dd x \\[2mm] + &\ {1 \over 2\verts{a}} \int_{\Lambda - \verts{a}}^{\Lambda + \verts{a}} {\cos\pars{x - \verts{a}} \over x}\,\dd x+ \pars{~\verts{a} \mapsto -\verts{a}~} \\[5mm] = &\ {1 \over 2\verts{a}}\int_{0}^{\Lambda - \verts{a}} {\cos\pars{x - \verts{a}} - \cos\pars{-x - \verts{a}} \over x}\,\dd x \\[2mm] + &\ {1 \over 2\verts{a}} \int_{\Lambda - \verts{a}}^{\Lambda + \verts{a}} {\cos\pars{x - \verts{a}} \over x}\,\dd x+ \pars{~\verts{a} \mapsto -\verts{a}~} \\[5mm] = &\ {\sin\pars{\verts{a}} \over \verts{a}}\ \underbrace{\int_{0}^{\Lambda - \verts{a}} {\sin\pars{x} \over x}\,\dd x} _{\ds{\to \color{red}{\large{\pi \over 2}}\ \mrm{as}\ \Lambda\ \to \infty}} \\[2mm] + &\ {1 \over 2\verts{a}}\ \underbrace{\int_{\Lambda - \verts{a}}^{\Lambda + \verts{a}} {\cos\pars{x - \verts{a}} \over x}\,\dd x} _{\ds{\color{red}{\Large\S :}\ \to \color{red}{\large 0}\ \mrm{as}\ \Lambda\ \to \infty}} + \pars{~\verts{a} \mapsto -\verts{a}~} \end{align}

---

Then, as $\ds{\Lambda \to \infty}$, \begin{align} &\bbox[5px,#ffd]{\mrm{P.V.} \int_{-\infty}^{\infty}{\cos\pars{x} \over a^{2} - x^{2}}\,\dd x} = {\pi\sin\pars{\verts{a}} \over 2\verts{a}} + {\pi\sin\pars{-\verts{a}} \over 2\pars{-\verts{a}}} \\[5mm] = &\ \bbx{\pi\,{\sin\pars{a} \over a}} \\ & \end{align}

---

$\ds{\color{red}{\Large\S :}}$ Note that \begin{align} 0 & < \verts{\int_{\Lambda - \verts{a}}^{\Lambda + \verts{a}} {\cos\pars{x - \verts{a}} \over x}\,\dd x} \\[5mm] & < \int_{\Lambda - \verts{a}}^{\Lambda + \verts{a}} {\dd x \over x} = \ln\pars{\Lambda + \verts{a} \over \Lambda - \verts{a}} \,\,\,\stackrel{\mrm{as}\ \Lambda\ \to\ \infty}{\to}\,\,\, \color{red}{\Large 0} \end{align}

Answer 3

The Cauchy Principal Value $$ \mathrm{PV}\int_{-\infty}^\infty\frac{\cos(x)}{a^2-x^2}\,\mathrm{d}x $$ is the integral along a path that looks like this

where the gaps on each side of the points are the same, infinitesimal, size.

To compute the integral along the disjoint contours above, we connect those contours with counter-clockwise semi-circles around the two singularities, which adds $\pi i$ times the sum of the residues at those singularities:

Note that $$\require{cancel} \begin{align} \operatorname*{Res}_{z=a}\left(\frac{\cos(z)}{a^2-z^2}\right) &=\operatorname*{Res}_{z=a}\frac1{2a}\left(\frac{\cos(z)}{a-z}+\cancel{\frac{\cos(z)}{a+z}}\right)\\ &=-\frac{\cos(a)}{2a} \end{align} $$ and $$ \begin{align} \operatorname*{Res}_{z=-a}\left(\frac{\cos(z)}{a^2-z^2}\right) &=\operatorname*{Res}_{z=-a}\frac1{2a}\left(\cancel{\frac{\cos(z)}{a-z}}+\frac{\cos(z)}{a+z}\right)\\ &=\frac{\cos(a)}{2a} \end{align} $$ Thus, the sum of the residues at the singularities is $0$.

We now write $\cos(z)=\frac{e^{iz}+e^{-iz}}2$ and close the contour with two huge semi-circles:

$\gamma^-$ consists of the bumpy contour along the real axis and lower (green) semi-circle. $$ \frac12\oint_{\gamma^-}\frac{e^{-iz}}{a^2-z^2}\,\mathrm{d}z=0 $$ since there are no singularities inside $\gamma^-$.

$\gamma^+$ consists of the bumpy contour along the real axis and upper (red) semi-circle. $$ \begin{align} \frac12\oint_{\gamma^+}\frac{e^{iz}}{a^2-z^2}\,\mathrm{d}z &=\frac12\oint_{\gamma^+}\frac{e^{iz}}{2a}\left(\frac1{a-z}+\frac1{a+z}\right)\mathrm{d}z\\ &=\frac{2\pi i}{4a}\left(-e^{ia}+e^{-ia}\right)\\[6pt] &=\frac\pi{a}\sin(a) \end{align} $$ Since the integrals along the semi-circular contours vanish as radius of the circle goes to $\infty$, we get that the integral along the bumpy, real-axis contour is $$ \int_\text{bumpy}\frac{\cos(z)}{a^2-z^2}\,\mathrm{d}z=\frac\pi{a}\sin(a) $$

The integral along the bumpy, real-axis contour is the principal value integral plus $\pi i$ times the sum of the residues at the singularities, which was $0$. Therefore, we get that $$ \bbox[5px,border:2px solid #C0A000]{\mathrm{PV}\int_{-\infty}^\infty\frac{\cos(x)}{a^2-x^2}\,\mathrm{d}x=\frac\pi{a}\sin(a)} $$

Answer 4

Real Approach $$\require{cancel} \begin{align} \mathrm{PV}\int_{-\infty}^\infty\frac{\cos(x)}{a^2-x^2}\,\mathrm{d}x &=\mathrm{PV}\int_{-\infty}^\infty\frac{\cos(x)}{2a}\left(\frac1{a-x}+\frac1{a+x}\right)\mathrm{d}x\tag1\\ &=\mathrm{PV}\int_{-\infty}^\infty\frac{\cos(x)}{a}\frac1{a+x}\,\mathrm{d}x\tag2\\ &=\mathrm{PV}\int_{-\infty}^\infty\frac{\cos(x)\cos(a)+\sin(x)\sin(a)}{a}\frac1{x}\,\mathrm{d}x\tag3\\[9pt] &=\frac{\cos(a)}a\,\underbrace{\mathrm{PV}\int_{-\infty}^\infty\frac{\cos(x)}x\,\mathrm{d}x}_0+\frac{\sin(a)}a\,\underbrace{\mathrm{PV}\int_{-\infty}^\infty\frac{\sin(x)}x\,\mathrm{d}x}_\pi\tag4\\ &=\pi\frac{\sin(a)}a\tag5 \end{align} $$ Explanation:
$(1)$: partial fractions
$(2)$: distribute then substitute $x\mapsto-x$ in the left sum
$(3)$: substitute $x\mapsto x-a$
$(4)$: distribute
$(5)$: integral of an odd function is $0$ and $\int_{-\infty}^\infty\frac{\sin(x)}{x}\,\mathrm{d}x=\pi$

---

Integral of Sinc

This can be tackled in a couple of real analytic ways. One is using equation $(9)$ of this answer. Another is $$ \begin{align} \int_{-\infty}^\infty\frac{\sin(x)}x\,\mathrm{d}x &=\color{#C00}{\sum_{k\in\mathbb{Z}}}\int_0^\pi\sin(x)\color{#C00}{\frac{(-1)^k}{x+k\pi}}\,\mathrm{d}x\tag6\\ &=\int_0^\pi\sin(x)\color{#C00}{\csc(x)}\,\mathrm{d}x\tag7\\[9pt] &=\pi\tag8 \end{align} $$ Explanation:
$(6)$: use $\sin(x+\pi)=-\sin(x)$
$(7)$: apply equation $(8)$ of this answer
$(8)$: integrate