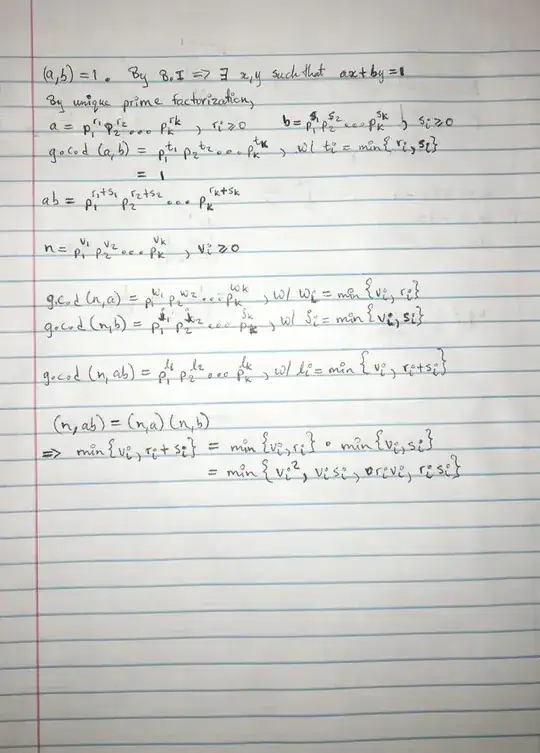1

My solution.

This is what I have been able to come up with so far.

I know that using Bezout's identity the g.c.d can be written into the sum of the products of two numbers (with a and b included). I also know that every number has a unique prime factorization, and to find the g.c.d you take the minimum value of the exponent for each prime number.

Additionally, I recognized that for the g.c.d of a and b to be 1, that means their prime factorization must include exponents raised to the zero power.

However, I am lost as to how to put all of this together to complete the proof.

CORRECTION For the last two lines it is supposed to be: min(v_i, r_i + s_i) = min(v_i, r_i) + min(v_i, s_i) and disregard the last line.

Tikwen
  • 17
  • 5
  • 1
    Here's a MathJax tutorial :) – Shaun Sep 25 '20 at 16:18
  • Thanks, I will try to make use of this next time but I don't think I really need it for this question. @Shaun – Tikwen Sep 25 '20 at 16:27
  • Why is it 'times' on the second-to-last line on your paper? Aren't you looking at exponents, which add? – Akiva Weinberger Sep 25 '20 at 16:58
  • That's true, I seemed to have overlooked that fact in my general confusion. @AkivaWeinberger – Tikwen Sep 25 '20 at 16:59
  • Also, if $p^{t_1}\dotsb {p_k}^{t_k}=1$, we have $t_i=0$, so $\min{r_i,s_i}=0$. That means, for any $i$, either $r_i=0$ or $s_i=0$. So each $i$ can be broken into two cases. – Akiva Weinberger Sep 25 '20 at 17:02
  • Yes, I was also thinking about that while trying to solve this problem. So, putting together the fact that the exponents are supposed to be added and that either r or s equals to zero for a particular i , this means that my last line would look like this: min(v,r) or min(v,s) for a particular i is equal to min(v,r) or min(v,s) for that same i ? – Tikwen Sep 25 '20 at 17:12
  • please use mathjax, that is part of minimum standards here. – jimjim Sep 25 '20 at 17:42
  • Just do it one prime at a time. If $p|a$ then $p\not \mid b$ and $p\not \mid \gcd(b,n)$ and if $k$ is the highest order that $p|a$ then $k$ is the highest power that $p|ab$ and if $m$ the highest order that divides $n$ then $\min(k,m)$ is the highest power that divides $\gcd(a,n)$ and the $\min(k,m)$ is the highest power that divides $\gcd(n,ab)$ and $\gcd(a,n)\gcd(b,n)$. If we do that for every prime.... we are done. – fleablood Sep 25 '20 at 20:41

2 Answers2

0

Let's consider only the primes where the exponents are greater than zero. Since a and b are coprime, your r's and your s's are disjoint and $min(v,r+s)$ is just either $min(v,r)$ or $min(v,s)$ You are mistaken in muliplying $min(v,r)$ and $min(v,s)$; they should be added, and you only get one or the other for a given prime, not both.

I don't think Bezout's inequality enters into it.

Anna Naden
  • 426
  • By looking at primes where the exponents are greater than zero, this means that r would be equal to zero for a given prime and s would be some number greater than zero (or vice versa). Is that what you are implying? And if so, then the g.c.d (n, ab) would either be min(v,r) or min(v,s) ? – Tikwen Sep 25 '20 at 17:05
  • The exponents of the gcd would be the minimum of the exponents in either n and a or n and b depending on whether the prime in question is a factor of a or a factor of b – Anna Naden Sep 28 '20 at 07:15
0

Let's make a teensy change to how we think of and express the unique prime factorization of a number.

If $p_k$ is the $k$th prime (so $p_1 = 2; p_2=3, etc.$) and for any natural number $m$ we will define $m_k$ as the non-negative integer (could be zero) that is the highest power of $p_k$ that divides $m_k$.

Then we can express the unique prime factorization of $m$ as $m = \prod\limits_{k=1}^{\infty} p_k^{m_k}$. And now that we've made that clear lets for the sake of typing assume the indexing of $1$ to $\infty$ is understood and we can write $m =\prod p_k^{m_k}$.

.....

Now a few things are immediate:

$\gcd(n,m) = \prod p_k^{\min (n_k,m_k)}$

$nm = \prod p_k^{n_k + m_k}$

$\gcd(n,m) =1$ implies that for any $k$ then either $n_k =0$ or $m_k=0$ (or, of course, both).

.....

Okay.... Now.... Let's just do it.

......

$\gcd(n,ab) = \prod p_k^{\min(n_k, a_k + b_k)}$

And $\gcd(a,n)\gcd(b,n) = \prod p_k^{(\min(a_k,n_k)+\min(b_k,n_k)}$.

And $\gcd(a,b)= 1$ so for all $k$ eithere $a_k =0$ or $b_k=0$.

So this is a matter of showing for each $k$ that $\min(n_k, a_k + b_k)=\min(a_k,n_k)+\min(b_k,n_k)$.

Now as $a_k = 0$ and $b_k =0$ so $a_k + b_k = a_k$ or $b_k$ whichever, if either, in non-negative (and therefore larger).

so $a_k + b_k = \max(a_k,b_k)$ and $\min(a_k,b_k) = 0$

So take cases:

......

Case 1: $n_k \ge \max (a_k, b_k) = a_k + b_k$.

The $\min(n_k,a_k+b_k) = a_k+b_k$ and $\min(a_k,n_k) +\min(b_k,n_k)= a_k + b_k$.

Case 2: $\min(a_k,b_k) = 0\le n_k < \max (a_k,b_k)$

Then $\min(n_k, a_k+b_k) =n_k$. And $\min(a_k,n_k) + \min(b_k,n_k)=$

Case 2a: $a_k = 0\le n_k <b_k$ then $\min(a_k,n_k) + \min(b_k,n_k) = a_k + n_k = 0+n_k = n_k$.

Case 2b: $b_k = 0 \le n_k < a_k$ then $\min(a_k,n_k) + \min(b_k,n_k)=n_k + b_k = n_k + 0 = n_k$.

That's it.

(Although it may seem a bit silly to note that for an infinite number of $k$ we are dealing with $n_k = a_k = b_k = 0$.)

fleablood
  • 124,253
  • Thanks, I think this together with the other post and comments has helped me to understand the concepts behind proving the answer and how to prove the answer. @fleablood – Tikwen Sep 25 '20 at 19:22