3

A basic limit question I don't quite understand... The question is as $$\lim_{x \to 5} \sqrt{x-5}$$ and solve for the limit.

When I plug in $5$ I get the answer zero, but when I tackle this question graphically the limit does not exist as nothing comes from the left of $5$.

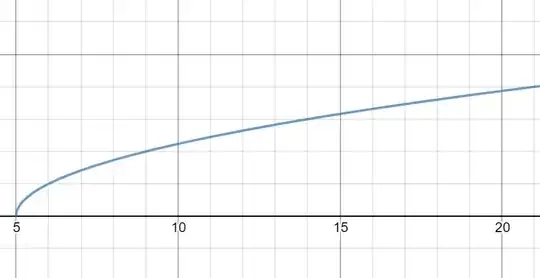
image of Graph

Could anyone clear this up for me? Thanks.

Blue
  • 75,673
realism98
  • 81
  • 1
  • 9
  • 1
    cf. one-sided limit – J. W. Tanner Sep 24 '20 at 13:11
  • There is no limit from the right, since the function is not defined for $x<5$, at least if you are talking about real numbers. – Andrei Sep 24 '20 at 13:11
  • 2
    $5$ is the left bound of the interval of definition of the function. Therefore, you just need to see what happens when $x$ tends to $5$ from the right. As you said, the function tends then to $0$, so you are allowed to say that the limit exists and is equal to $0$. – TheSilverDoe Sep 24 '20 at 13:21
  • 1
    @Andrei you mean there is no limit from the left. The limit from the right exists because the function is defined for $x\gt 5$ – Radial Arm Saw Sep 24 '20 at 15:02
  • 2
    @TheSilverDoe No- the limit stated in the question does not exist, because if there is no + or - next to the limit then the limit is taken from both sides. – Radial Arm Saw Sep 24 '20 at 15:03
  • 3
    @RadialArmSaw In the usual definition of the limit, when you write $x \rightarrow 5$, that means that $x$ tends to $5$ while belonging to the domain of $f$. So the limit does exist. Please see Yves Daoust's answer. – TheSilverDoe Sep 24 '20 at 15:05
  • 1
    The limit does not exist since a requirement is that we can approach from the left AND from the right and both limits exist and coincide. That the function is not defined for $x<5$ does not change this requirement. But the limit from the right exists. Hence, as written above, it does NOT exist. – Peter Sep 24 '20 at 15:13
  • 1
    @Peter So would you say that $x \mapsto 1/x$ does not have a limit when $x$ tends to $+\infty$ because you cannot approach $+\infty$ from the right ??? – TheSilverDoe Sep 24 '20 at 15:18
  • Of course, what I said applies only to a limit to a finite value. The limit to $\infty$ or $-\infty$ is something different. – Peter Sep 24 '20 at 15:22
  • 1
    @Peter It should not. If you want a consistent definition of the limits, there is only one way, which is the following definition : "$f(x)$ tends to $l$ when $x$ tends to $a$ if for every neighborhood $U$ of $l$, there exists a neighborhood $V$ of $a$ such that for every $y$ belonging to $V \cap$ domain $(f)$, $f(y)$ belongs to $U$". – TheSilverDoe Sep 24 '20 at 15:42
  • 1
    @TheSilverDoe Infinity is not a number, so approaching from both sides doesn’t apply there. – Radial Arm Saw Sep 24 '20 at 15:54
  • 1
    @RadialArmSaw Thank you. – Peter Sep 24 '20 at 16:00
  • 1
    @Peter and RadialArmSaw Please read the first comment (Daniel Fischer's) on the link provided by Hans Lundmark. – TheSilverDoe Sep 24 '20 at 16:08
  • 1
    @AlexLee Exactly this is the issue with this situation. Some argue that we need not the limit from the left because the function is not at all defined there. Maybe, this is a "convention", but I think a debatable one. – Peter Sep 24 '20 at 16:10
  • @TheSilverDoe I read Yves’s answer but I don’t see how it disproves my statement. – Radial Arm Saw Sep 24 '20 at 16:12
  • 1
    @RadialArmSaw Well, according to Yves's answer, the function has a limit, whereas you say that it has not... – TheSilverDoe Sep 24 '20 at 16:13
  • @TheSilverDoe He mentioned a requirement of the definition of the limit but he didn’t mention other requirements. – Radial Arm Saw Sep 24 '20 at 16:17
  • 1
    @RadialArmSaw Yves just says that the correct definition of the sentence "$f$ tends to $L$ when $x$ tends to $c$" is : $\forall \varepsilon >0$, there exists $\delta >0$ such that $\forall x \in$ dom $(f) \setminus \lbrace c \rbrace$, one has the implication $|x-c| < \delta \Rightarrow |f(x)-L| < \varepsilon$. I am sure that you are able to understand by yourself why, with this correct definition, there is no debate on the fac that $\sqrt{x-5}$ does have a limit when $x$ tends to $5$. – TheSilverDoe Sep 24 '20 at 16:23

3 Answers3

5

It is a common mistake to forget an essential aspect of the definition of the limit: the constraint $|f(x)-L|<\epsilon$ must hold $\forall x\color{red}{\in\text{dom}(f)\setminus\{c\}}:|x-c|<\delta$.

0

While $\lim_{x\to5^+}\sqrt{x-5}=0$ only requires the theory of real numbers, $\lim_{x\to5^-}\sqrt{x-5}=0$ requires us to work with complex values of the square root, e.g. with the convention $\sqrt{-k^2}=ki$ for all $k>0$. It's possible any software that said $\lim_{x\to5}\sqrt{x-5}=0$ knows how to use this approach.

J.G.
  • 115,835
  • If you allow complex values of $\sqrt{x}$ then you should also allow complex $x$. Then $\lim_{z\to 5} \sqrt{z-5}$ has to consider all approaches to $z=5$ in the complex plane. – Christoph Sep 24 '20 at 13:32
  • 1
    In the reals, the ordinary limit $\lim_{x\to5}\sqrt{x-5}=0$ indisputably holds, by the definition. –  Sep 24 '20 at 13:34
  • @Christoph We don't have to have the same allowed $x$ as $\sqrt{x-5}$, as the issue is making the function well-defined in a neighbourhood, which can be restricted to $\Bbb R$. But if we do allow complex $x$, it works as long as we decide how to define square roots in general. – J.G. Sep 24 '20 at 13:48
0

The notation $$\lim_{x\to 5}\sqrt{x-5}$$ is somewhat ambiguous because it doesn't tell us about the domain of the function given by the formula $$f(x)=\sqrt{x-5}$$ Knowing the domain of the function under the limit is necessary to determine the limit or state that it doesn't exist.

Assuming that the domain is maximal possible i.e. $$D=[5,\infty),$$

the limit exists and is equal to zero. For explanation refer to the limit definition.

Kulisty
  • 1,468
  • It suffices that $5$ be a limit point of the domain. $D={n\in\mathbb N:5+\frac1n}$ would work. –  Sep 24 '20 at 13:37
  • @YvesDaoust What do you mean by "would work"? If no domain is given, one usually assumes the maximal possible domain. So in the context of real numbers the term $\sqrt{x-5}$ would come with the implied domain $D=[5,\infty)$. In the context of complex numbers we would assume $D=\mathbb C$ in the definition of $\lim_{z\to 5} \sqrt{z-5}$. – Christoph Sep 24 '20 at 13:43
  • @Christoph: I mean that with this $D$ the limit would exist. Any objection ? –  Sep 24 '20 at 13:44
  • No objection to that, but I don't see how that's relevant to either the question or the answer. – Christoph Sep 24 '20 at 13:45
  • The limit doesn’t exist because you can’t approach from both sides of $x=5$. If there is no + or - sign next to the limit then you have to approach from both sides. – Radial Arm Saw Sep 24 '20 at 16:10