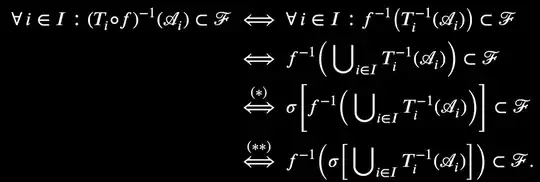0

Let $X$ be a set, let $\left(X_{i}, \mathscr{A}_{i}\right), i \in I,$ be arbitrarily many measurable spaces and let $T_{i}: X \rightarrow X_{i}$ be a family of maps. Show that a map $f$ from a measurable space $(F, \mathscr{F})$ to $\left(X, \sigma\left(T_{i}: i \in I\right)\right)$ is measurable if, and only if, all maps $T_{I}\circ f$ are $\mathscr{F} / \mathscr{A}_{i}$ -measurable.

Which results (e.g. theorem, lemma etc.) does make the last biimplication possible in the solution below: enter image description here

Sorry
  • 1,028
  • 1
    I think there is a typo in your question: it should be "...if and only if all maps $T_i\circ f$ are $\mathscr{F}/\mathscr{A}_i$ -measurable." – Mittens Sep 24 '20 at 15:52

2 Answers2

0

There is a general statement saying that $$\sigma(f^{-1}(\mathcal{G})) = f^{-1}(\sigma(\mathcal{G}))$$ for any collection of sets $\mathcal{G}$ (see here for a proof). Applying this for $$\mathcal{G} := \bigcup_{i \in I} T_i^{-1}(\mathcal{A}_i)$$ proves the last equivalence in the solution.

saz
  • 120,083
  • Thanks. How does $$f^{-1}\left(\bigcup_{i \in I} T_{i}^{-1}\left(\mathscr{A}{i}\right)\right) \subset \mathscr{F} \iff \sigma\left[f^{-1}\left(\bigcup{i \in I} T_{i}^{-1}\left(\mathscr{A}_{i}\right)\right)\right] \subset \mathscr{F}$$

    Follow? Which definition is this?

     – Sorry Sep 25 '20 at 10:42
  • Do not understand how it follows from left to right. – Sorry Sep 25 '20 at 10:57
  • @Xenusi If $\mathcal{H}$ is any system of sets and $\mathcal{F}$ is an $\sigma$-algebra, then $\mathcal{H} \subseteq \mathcal{F}$ implies $\sigma(\mathcal{H}) \subseteq \mathcal{F}$ (note that, by definition, $\sigma(\mathcal{F})$ is the smallest $\sigma$-algebra containing $\mathcal{H}$, and from $\mathcal{H} \subseteq \mathcal{F}$ we see that $\mathcal{F}$ is a $\sigma$-algebra containing $\mathcal{H}$). Applying this for $\mathcal{H} := f^{-1} \left( \bigcup_i T_i^{-1}(\mathcal{A}_i) \right)$ proves "$\Rightarrow$". – saz Sep 25 '20 at 11:36
0

Hint:

The problem with the OP is with notation. Before getting drown with notation, notice that a solution to the OP follows from the following result

Lemma: Suppose $\mathscr{G}$ is a collection of subsets of $X$ and $\mathscr{H}=\sigma(\mathscr{G})$ (i.e. $\mathscr{H}$ is the $\sigma$-algebra generated by $\mathscr{G}$). Let $(F,\mathscr{F})$ be measure space. A function $f:F\rightarrow X$ is $\mathscr{F}/\mathscr{H}$ measurable iff $f^{-1}(G)\in\mathscr{F}$ for all $G\in\mathscr{G}$.

Note: This result says that it is enough to test on the generators to check for measurability. Similar to what one does for real value functions: $X:(F,\mathscr{F})\rightarrow\mathbb{R}$ is Borel-measurable iff $X^{-1}((-\infty,a))\in\mathscr{F}$ for all $a\in\mathbb{R}$.

Here is a short proof of the Lemma:

On on direction is easy: $f$ measurable implies $f^{-1}(H)\in\mathscr{F}$ for all $H\in\mathscr{H}$. Hence $f^{-1}(G)\in\mathscr{F}$ for all $G\in \mathscr{G}$ ($\mathscr{G}\subset\mathscr{H})$.

On the other direction: Notice that the collection $\mathcal{A}:=\{A\subset X: f^{-1}(A)\in\mathscr{F}\}$ is a $\sigma$-algebra. It contains $\mathscr{G}$ and so, $\mathscr{H}=\sigma(\mathscr{G})\subset\mathcal{A}$ ($\mathscr{H}$ is the smallest $\sigma$-algebra containing $\mathscr{G}$). Thus $$\sigma(\{f^{-1}(G):G\in\mathscr{G}\}=\{f^{-1}(H):H\in\sigma(\mathscr{G})\}\subset\mathscr{F}$$

For the OP,

  • Take $\mathscr{G}=\{T^{-1}_i(A): i \in I,\,A\in\mathscr{A}_i\}=\bigcup_{I\in I}\{T^{-1}_i(A):A\in\mathscr{A}_i\}$, and set $\mathscr{H}=\sigma(\mathscr{G})$.
  • $f:F\rightarrow X$ is $\mathscr{F}/\mathscr{H}$ measurable if and only if $f^{-1}(T^{-1}_i(A))$ for all $i\in I$, $A\in\mathscr{A}_i$.
  • Notice that $f^{-1}(T^{-1}_i(A))=(T_i\circ f)^{-1}(A)$ for all $i\in I$ and $A\in \mathscr{A}_i$.
  • Thus, $f$ is $\mathscr{F}/\mathscr{H}$ measurable iff $T_i\circ f$ is $\mathscr{F}/\mathscr{A}_i$ measurable for any $i \in I$.

On natation:

Sometime in the literature, the following notation is used:

  • Given a collection of subsets $\mathscr{G}$ of $X$, $f^{-1}(\mathscr{G}):=\{f^{-1}(G): G\in\mathscr{G}\}$.
  • The Lemma above is denoted as $f$ is $\mathscr{F}/\sigma(\mathscr{G}$ measurable iff $f^{-1}(\sigma(\mathscr{G}))=\sigma(f^{-1}(\mathscr{G}))\subset\mathscr{F}$.
Mittens
  • 39,145