$\min_{b \in \mathbb R}(| a_1−b |+ | a_2−b |+\dots+ | a_m−b |)$ .

Question

Let $a_1, a_2, . . . , a_m$ be $m$ given real numbers.

(a) Prove that the mean of $a_1, a_2, . . . , a_m$ minimizes $(a_1−b)^2+ (a_2−b)^2+\dots+ (a_m−b)^2$ over all $b \in \mathbb R$ .

(b) Prove that a median of $a_1, a_2, . . . , a_m$ minimizes $|a_1−b|+|a_2−b|+\dots+|a_m−b|$ over all $b \in \mathbb R$.

Can theses problems be done using inequalities and not getting into calculus? Can anyone please give me some hints?

Answer 1

(b)

Without loss of generality, suppose $a_1\leq a_2\leq \cdots\leq a_m$.

We can easily notice that $\left|b-a_1\right|+\left|b-a_m\right|$ has the minimal value (which is $a_m-a_1$) when $a_1\leq b\leq a_m$.

Do this again with $a_2$ and $a_{m-1}$ , you get $a_2\leq b \leq a_{m-1} $. With $a_3$ and $a_{m-2}$ , you get $a_3\leq b \leq a_{m-2}$ , and so on.

Eventually you are going to find that $b$ has to be the median of $a_1,a_2,\cdots,a_m$ so that $b$ can minimize the sum.

For (a) I'm not too sure, but I think that the solutions can be similar.

Answer 2

For (a) you have $$(a_1-b)^2+\cdots+(a_n-b)^2=A-2Mb+nb^2$$ where $A=a_1^2+\cdots+a_n^2$ and $M=a_1+\cdots+a_n$. You are minimising a quadratic function. Perhaps complete the square?

Answer 3

The function

$$f(b)=|b-a|$$ is piecewise linear with a slope $-1$ for $b<a$ and $+1$ for $b>a$.

So a sum like

$$\sum_{k=1}^n|b-a_k|$$ is piecewise linear, with changes of slope at every $a_k$. And the slope at a given point $b$ is the difference of the number of $a_k$ values to its right and the number of $a_k$ values to its left.

(In fact the derivative rule works, with

$$f'(b)=\sum_{k=1}^n\text{sgn}(b-a_k),$$

though as it is not defined at the $a_k$, you need to find the global change of sign instead.)

Hence, the minimum is achieved "in the middle". Depending on the parity of $n$, the minimum is a single point or an interval. (Check the slopes $-3,-1,1,3$ and $-4,-2,0,2,4$.)

---

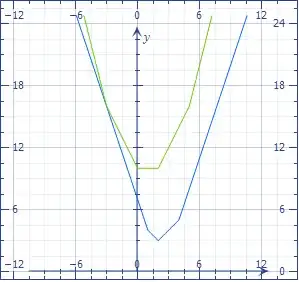
The quadratic case is somewhat easier, as the quadratic trinomials add up.

$$\sum_{k=1}^n(b-a_k)^2=nb^2-2\sum_{k=1}^na_k\,b+\sum_{k=1}^na_k^2.$$

You can find the minimum by differentiating.

$$2nb-2\sum_{k=1}^na_k=0\implies b=\dfrac1n\sum_{k=1}^na_k.$$

Or by completing the square.