1

Prove by mathematical induction that:

1. for all n ≥ 3 equality $$\binom{3}{3}+\binom{4}{3}+ · · · +\binom{n} {3}=\binom{n+1} {4};$$

2. for all n ≥ 1 equality $$\binom{2}{2}+\binom{3}{2}+ · · · +\binom{n+1} {2}=\binom{n+2} {3}$$

So for the two exercises, I have to apply the binomial coefficient of $$\binom{n}{m}= \frac{n!} {m!(n−m)!} =\frac{(n-1)...(n−m+1)}{m!}$$

This the solution for the first exercise before dividing both sides to (k + 1)k(k− 1)/4!.

enter image description here

And my question is why when I solved the first exercise my answer was:

$$\frac{(k+1)k(k+2)} {4!} + \frac{(k+1)k(k-1)} {3!} = \frac{k+2(k+1)(k-1)} {4!}$$

What is the step I'm missing ?

Marita
  • 25
  • 4
  • It should be ${n\choose m}=\frac{n!}{m!(n-m)!}=\frac{n\cdot(n-1)\cdot\cdot\cdot(n-m+1)}{m!}.$

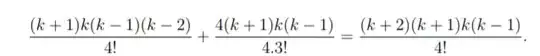
    So for the first problem assume it holds for $n=k$ then for the inductive step $$\binom{3}{3}+\binom{4}{3}+ · · · +\binom{k} {3}+\binom{k+1}{3}=\binom{k+1} {4}+\binom{k+1}{3}$$ $$=\frac{(k+1)!}{4!(k-3)!}+\frac{(k+1)!}{3!(k-2)!}$$ $$=\frac{(k+1)k(k-1)(k-2)}{4!}+\frac{(k+1)k(k-1)}{3!}$$ $$=\frac{(k+1)k(k-1)(k-2)+4(k+1)k(k-1)}{4!}$$ $$=\frac{(k+1)k(k-1)[(k-2)+4]}{4!}=\frac{(k+2)(k+1)k(k-1)}{4!}$$ $$=\frac{(k+2)!}{4!(k-2)!}=\binom{k+2}{4}$$

     – Alessio K Sep 22 '20 at 18:09

1 Answers1

0

In both cases, the inductive step boils down to Pascal's relation $\binom{k+1}{r+1}+\binom{k+1}{r}=\binom{k+2}{r+1}$, which you can prove with factorials or a double-counting argument. (If you prove it with a double-counting argument, you can thereafter derive the expression for binomial coefficients in terms of factorials, & vice versa.) You chose the factorial-based approach. After correcting a typo in the first fraction of your final calculation for problem 1,$$\begin{align}\frac{(k+1)k(k-1)(k-2)}{4!}+\frac{(k+1)k(k-1)}{3!}&=\frac{(k+1)k(k-1)}{4!}(k-2+4)\\&=\frac{(k+2)(k+1)k(k-1)}{4!}.\end{align}$$

J.G.
  • 115,835