1

SQUARE ROOT

Let's say that I have:

\begin{align*} x^2 &= 9 \end{align*}

And I $\sqrt{\phantom{x}}$ an entire equation to get:

\begin{align*} x_{1,2} &= \sqrt{9}\\ x_{1} &= +3\\ x_{2} &= -3 \end{align*}

Experience and "fundamental theorem of algebra" thought me that:

There are always two square roots ($x_1$, $x_2$)!

Experience thought me that:

Product of mixed roots doesn't return back the original: \begin{align*} x_1 \cdot x_2 &= -3 \cdot 3 = -9\\ x_2 \cdot x_1 &= 3 \cdot (-3) = -9 \end{align*}

Experience also thought me that:

Only if roots are multiplied by itself they return back the result: \begin{align*} x_1 \cdot x_1 &= 3 \cdot 3 = 9\\ x_2 \cdot x_2 &= (-3) \cdot (-3) = 9 \end{align*}

CUBE ROOT

Then there comes this:

\begin{align*} x^3 &= 1\\ \end{align*}

If I $\sqrt{\phantom{x}}$ an entire equation I get:

\begin{align*} x_{1,2,3} &= \sqrt[3]{1}\\ x_1 &= 1\\ x_2 &= \text{???}\\ x_3 &= \text{???} \end{align*}

Here I have no experience whatsoever but "fundamental theorem of algebra" says that:

There are always three cube roots ($x_1$, $x_2$, $x_3$)!

Now pay attention! Like for square root it should be true that:

If roots $x_1$, $x_2$, $x_3$ are multiplied by itself they return $1$. Their mixed products will probably return something else. \begin{align*} x_1 \cdot x_1 \cdot x_1 = 1\\ x_2 \cdot x_2 \cdot x_2 = 1\\ x_3 \cdot x_3 \cdot x_3 = 1 \end{align*}

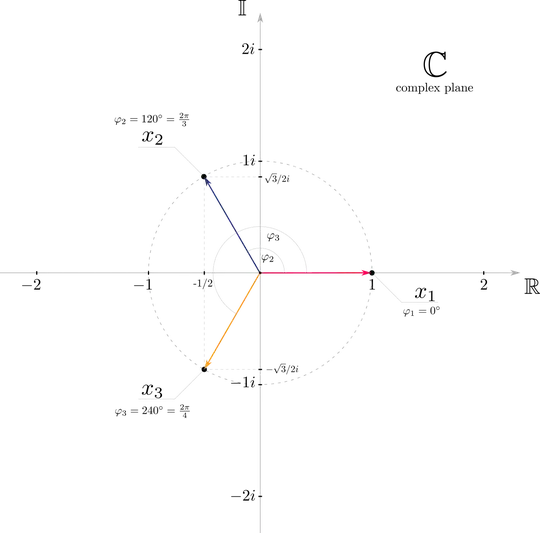
So at this point everybody's already rushing to their paper and drawing this complex plane:

enter image description here

And in complex plane:

If we multiply complex numbers, length of their position vectors multiply and their angles sum up.

So everybody will now draw $x_1$ on the $\mathbb{R}$ axis and tell me that this is the first root. I agree with that. Then they say:

Length of a position vector of other two roots ($x_2$, $x_2$) must be $1$ as well.

And I agree with that. But what they say now, I can't agree with no matter how I look at it. They say:

Because according to "fundamental theorem of algebra" there are three cube roots, and we will multiply them in order to get to $1$, angle between them must be $120^\circ$. We now start at $1$ and if we do a full circle we end at $1$ again. Woila! Problem solved...

I can't agree with this explanation as is because this only holds for $x_1$. If I take $x_1$ and make a full circle I end up getting $1$. But with $x_2$ and $x_3$ my starting point is not $1$. Starting points are actually:

\begin{align*} \text{starting point for $x_2$:} \hspace{5mm} -\frac{1}{2} - \frac{\sqrt{3}}{2}i \\ \text{starting point for $x_3$:} \hspace{5mm} -\frac{1}{2} + \frac{\sqrt{3}}{2}i \end{align*}

And in case of $x_2$ and $x_3$ when we do a full circle we don't end up getting $1$, but we geometricaly looking end at positions:

\begin{align*} -1/2 - \sqrt{3}/2 i \\ -1/2 + \sqrt{3}/2 i \end{align*}

If the starting positions are as I state they are, angle that we need in order to get to the $1$ should be $\pm240/3 = \pm80^\circ$.

But then why does this explanation that they use, work? At the end of the day e.g. $x_2$ solves the problem:

\begin{align*} \left(x_2\right)^3 &= 1\\ \left( -\frac{1}{2} + \frac{\sqrt{3}}{2} i \right)^3 &= 1\\ \left( -\frac{1}{2} + \frac{\sqrt{3}}{2} i \right) \left( -\frac{1}{2} + \frac{\sqrt{3}}{2} i \right) \left( -\frac{1}{2} + \frac{\sqrt{3}}{2} i \right)&= 1\\ \left(\frac{1}{4} - \frac{\sqrt{3}}{4}i - \frac{\sqrt{3}}{4}i + \frac{3}{4}i^2\right) \left( -\frac{1}{2} + \frac{\sqrt{3}}{2} i \right) &= 1\\ \left(\frac{1}{4} - \frac{2\sqrt{3}}{4}i - \frac{3}{4}\right) \left( -\frac{1}{2} + \frac{\sqrt{3}}{2} i \right) &= 1\\ \left(-\frac{1}{2} - \frac{\sqrt{3}}{2}i\right) \left( -\frac{1}{2} + \frac{\sqrt{3}}{2} i \right) &= 1\\ \frac{1}{4} - \frac{\sqrt{3}}{4} i + \frac{\sqrt{3}}{4} i - \frac{3}{4} i^2 &= 1\\ \frac{1}{4} + \frac{3}{4} &= 1 \end{align*}

I am sure there is something wrong with the explanation everybody are using but it is correct to assume roots are $120^\circ$ appart...

Probably the point here is not about making a full circle at all! Like most of the people say. It must be about adding conjugate pairs so that artifficialy we create enough roots to satisfy fundamental theorem of algebra! Thats all! So odd number root $3$ was historicaly first one that forced us to get out of the horizontal axis in complex plane and invent complex roots...

Can anyone present a proper explanation of why we choose $120^\circ$ for cube roots?

71GA
  • 841
  • In the first case, $x_2\cdot x_2=9$, not $-9$. –  Sep 21 '20 at 20:53
  • This is pretty much impossible to understand why $120^{\circ}$ without using polar form. Are you familiar with it? – Olivier Moschetta Sep 21 '20 at 20:54
  • For the square root, technically it's $$\begin{align} x_{1,2} &=\pm \sqrt{9}\ x_{1} &= +3\ x_{2} &= -3 \end{align}$$ The square root by definition returns the positive solution. Which is to say it always gives only $x_1$. Never $x_2$, never both. – Arthur Sep 21 '20 at 20:58
  • @Arthur: which is the positive square root of $-1$? Or of $-i$? – Henry Sep 21 '20 at 21:04
  • https://math.stackexchange.com/questions/192742/how-to-solve-x3-1 – lab bhattacharjee Sep 21 '20 at 21:08
  • @Henry Neither. Which is why you will basically never see me write $\sqrt{-1}$ or $\sqrt i$, except in two specific circumstances: 1) Discussing this very issue, and 2) The quadratic formula, just because everyone's a little hypocritical. (I'm sure if you dig around, you can find me using roots like this in the past. But it's been a while now, and I have lost nothing of value. When convenient and relevant, I always suggest to anyone and everyone that they too stop using the square root on negative or non-real numbers.) – Arthur Sep 21 '20 at 22:09
  • @user798202 I fixed the $x_2 \cdot x_2 = 9$ typing error. – 71GA Sep 22 '20 at 03:52
  • @OlivierMoschetta I am familiar with a polar form. $x_1 = 1 \angle 0^\circ$, $x_2 = 1 \angle 120^\circ$, $x_3 = 1 \angle 240^\circ$. I know that when multiplied the lengths are multiplied and angles are summed. – 71GA Sep 22 '20 at 03:56

1 Answers1

1

There is really no "first" root, "second" root, etc.

In the case of $x^2=1$, there are two roots, $-1$ and $1$. It is your choice to give these two roots whatever names you like.

In the case of $x^3=1$, there are three distinct roots. Again, it does not matter which one you call $x_1$.

In general, (complex) solutions to the equation $x^n=1$ together with complex multiplication form a group: https://en.wikipedia.org/wiki/Root_of_unity

This group tells you what happens when you multiply two solutions to the equations $x^n=1$.

I don't know where the "everybody explanation" is from; I would not do that anyway.

One way to find the three roots for $x^3=1$ is quite straightforward. Write $x=re^{i\theta}$ where $r\ge 0$ and $\theta\in[0,2\pi)$. Then

$$ (re^{i\theta})^3=1 $$ Taking the absolute value on both sides you get $r=1$. On the other hand, $$ e^{i(3\theta)}=1 $$ which implies that $3\theta=2k\pi$ where $k$ is some integer. Now write $$ \theta=\frac{2k\pi}{3},\quad k\in\mathbb{Z} $$ and pick the ones that are in $[0,2\pi)$. By periodicity, this is not a unique way to represent the roots. You could, for example, restrict $\theta$ to $[-\pi,\pi)$ at the beginning of the calculation.