I understand a continuous function may not be differentiable. But does every continuous function have directional derivative at every point? Thanks!
-
2A continuous not differentiable function on $\mathbb R$ will be a counterexample. – Arctic Char Sep 21 '20 at 17:29
-
1@OlivierMoschetta That is not correct, one needs some sort of uniformity. – copper.hat Sep 21 '20 at 17:43
-
2The function $f(x) = \sqrt{|x|}$ is continuous but does not have a directional derivative at $x=0$. – copper.hat Sep 21 '20 at 17:44
-
1Hint: In one dimension, the derivative is a directional derivative. – John Douma Sep 21 '20 at 17:52
-
1In fact, there exist continuous functions from ${\mathbb R}^n$ to $\mathbb R$ such that, at EACH point, NONE of the directional derivatives exist at that point. An example for $n=2$ (which can be easily adapted for larger values of $n)$ is given in Theorem 4 on p. 973 of Crinkly curves and choppy surfaces by Felix Adalbert Behrend. (continued) – Dave L. Renfro Sep 21 '20 at 18:04
-
1As one might expect, most continuous functions have this property, where "most" can be almost everywhere the sense of Baire category (I don't know of a published proof of only this result, but a stronger version based on $\sigma$-porous sets is given here) and "most" can be almost everywhere in the sense of Weiner measure (see this paper). – Dave L. Renfro Sep 21 '20 at 18:04
-
1@Tavin I am not sure what you are asking. The function I mentioned in my comment has no one sided directional derivative in any direction (other than $0$). – copper.hat Jul 16 '23 at 21:26
2 Answers
No. Consider the function $f(x,y) = e^{-\sqrt{x^2+y^2}}$. Then $f$ is continuous everywhere, but $f(0,0)$ has no directional derivative at $(0,0)$. I'll let you prove this rigorously on your own, but this should be clear from the plot below; the graph is obviously not differentiable at the "tip". 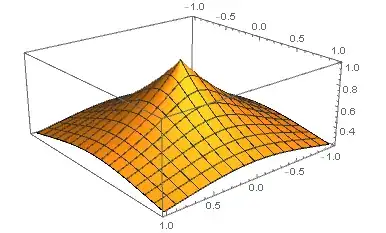
- 1,078
-
Approaching the origin from any angle, the slope has a limit. What is that value if not a directional derivative? – Tavin Jul 16 '23 at 21:20
There is no need to distinguish between one and more directions. If a continuous function like $x\longmapsto |x|$ isn't differentiable at $x=0,$ then there is no directional derivative in $x$-direction.
The contrary is the case: every differentiation is always a directional differentiation. We have that $f$ is differentiable at $x_0$ if there is a linear function $\mathbf{J}$ and a remainder function $\mathbf{r}$ such that
\begin{equation}\mathbf{f(x_{0}+v)=f(x_{0})+J(v)+r(v)} \end{equation}
where $\mathbf{v}$ is the direction where we consider a change of slope. Partial derivatives are along the coordinate axis, the total derivative is a linear combination of partial derivatives, but all are in some direction $\mathbf{v}$.
- 2,245