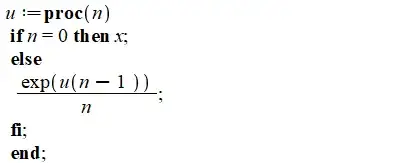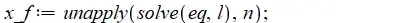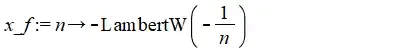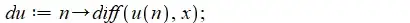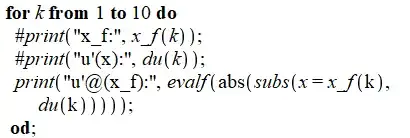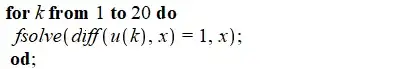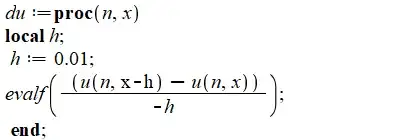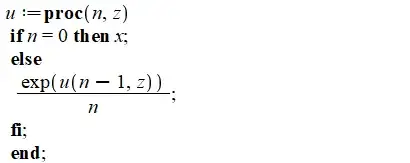$u_{n+1}=\frac{e^{u_n}}{n+1}$

Question

One can prove that for $x\in \mathbb{R}$, the sequence $$ u_0=x\text{ and } \forall n\in \mathbb{N},\qquad u_{n+1}=\frac{e^{u_n}}{n+1} $$ converges to $0$ if $x \in ]-\infty,\delta[$ and diverges to $+\infty$ if $x\in ]\delta,+\infty[$ for a fixed $\delta$. I'm trying to find more information on the value $\delta$ (inequalities or expression) and on the specific sequence $$ u_0=\delta \text{ and } \forall n\in \mathbb{N},\qquad u_{n+1}=\frac{e^{u_n}}{n+1} $$ Any reference or help are welcome. The only thing I can prove at the moment is $\ln \ln 2 \le \delta \le 1$.

Answer 1

Numerical results:

It seems that $\delta\approx0.3132776395465557$. This was computed using root-finding techniques to find when $u_n=y$ for $y=0.1,1,10$ and $n=10,100,1000$. Code here.

Proofs of bounds:

Disclaimer: Proof that the bounds are tight is not given, but is supported numerically.

Lower bounds can be proven by observing when $t=u_n=u_{n-1}$ occurs. If this occurs, then all future iterations are clearly decreasing. Solving for this gives

$$t=\frac1ne^t\implies t=-W_{-1}\left(-\frac1n\right)$$

where $W_{-1}$ is the real branch of the Lambert W function which gives the largest value for $t$. Working backwards from this point to find $x$ then gives

$$x=\ln\left(1\cdot\ln\left(2\cdot\ln\left(\dots(n-1)\cdot\ln\left(-nW_{-1}\left(-\frac1n\right)\right)\dots\right)\right)\right)$$

$\delta$ is then at least the supremum of this. Note that there are no solutions for $t<3$. The first few values of this lower bound is given by

$$\begin{array}{c|c}n&\delta\ge{}?\\\hline3&0.1013550034887759\\4&0.2751555022435671\\5&0.3044035425578071\\10&0.3132705224120361\\20&0.3132776395448800\\30&0.3132776395465558\end{array}$$

Note that $n=30$ corresponds to the estimated $\delta$ approximation. See also the code above.

Upper bounds can be shown in a similar manner by solving $u_n=u_{n-1}+1\ge3$, which gives

$$u_{n+1}=\frac1{n+1}e^{u_n}=\frac{en}{n+1}\cdot\frac1ne^{u_{n-1}}=\frac{en}{n+1}\cdot u_n\ge u_n+1$$

and is thus diverges to $\infty$. (Again see code above).

It appears to be the case that these bounds are asymptotically tight. Proving so seems to be rather messy, however.

Answer 2

My numerics agree with Simply's result. Here's a little Maple code:

Define $u_n(x)$:

At the $n$-th iteration the limit (if it exists) is given by solving: $l=\exp(l)/n$:

so the fixed point at this level is given (as a function of $n$) by:

That is:

the derivative $du_n(x)/dx$ (as a function of $n$):

And now just check the iterates $|u_n'(x_f)|$:

                "u'@(x_f):", 1.374557011
                "u'@(x_f):", 5.413650945
                "u'@(x_f):", 48.78006459
                "u'@(x_f):", 29.62255784
                "u'@(x_f):", 14.17327019
                "u'@(x_f):", 2.493811293
               "u'@(x_f):", 0.2768959061
               "u'@(x_f):", 0.02871591627
              "u'@(x_f):", 0.002877744731
              "u'@(x_f):", 0.0002733561570

Although $|u_n'(x_f)|$ oscillates some in the beginning, the above is a strong indication that the fixed points are becoming super-attractors. So now conversely simply iterate the numerical solutions to $u_n'(x)=1$ to pick a good bound for the initial $x$:

With 20 iterates, I get:

                           0.
                     -0.1594583215
                     -0.1858157472
                     -0.1022224792
                     0.03068160157
                      0.1493286247
                      0.2282136125
                      0.2723541387
                      0.2946085552
                      0.3050959095
                      0.3098066970
                      0.3118452094
                      0.3127005207
                      0.3130500940
                      0.3131896678
                      0.3132442219
                      0.3132651501
                      0.3132730435
                      0.3132759718
                      0.3132770420

which agrees to 7 dec with Simply's answer.

Note: That's the code for estimating $\delta$. If you have symbolics for the derivative of functions, it's much easier, but if you don't, just code your function for the derivative of $u_n$ up to level $n$ (for accuracy to level $n$) as $g(x)$ and numerically solve the equation $g(x)=1$. For example, for accuracy to level 2, your $u_2(x)=1/2\exp(\exp(x))$, so code an estimate for the derivative as: $g(x)=\frac{u_2(x+h)-u_2(x)}{h}$, for small $h$ (say $\sim 0.01$ or similar). Then numerically solve the equation: $g(x)=1$. The estimate of course depends on how high your $n$ is and how small your $h$ is. The higher the $n$ and the smaller the $h$, will improve the numerical solutions found when solving $g(x)=1$. The Maple code above, does all this automatically. After you get an estimate for $\delta$, you can verify that $u_n(\delta)$ converges and $u_n(\delta+dx)$ diverges for most $dx\ge\epsilon\gt 0$.

Addendum to Note #2: If you don't have a symbolic calculator, the above can be a bit of a nuisance to code in low level . The reason being that the equation $u_n'(x)=1$ needs to be solved numerically. The usual way to solve this is to look for roots of $g(n,x)=u_n'(x)-1$ by implementing some sort of numerical root finder, such as Newton's method. The problem is that Newton's method causes overshoots with this $u_n$ and as a result it does not converge. Halley's method will overshoot, too (the derivative $u_n'(x)$ may become unbounded). So, a good method to solving $u_n'(x)=1$, numerically would be the bisection method, like Simply uses. Here's then some low level code which you can translate directly if you don't feel like translating his code, to obtain some estimates for $ \delta$. Assuming you have defined your $u_n(x)$ as above in this post, code an approximation of its derivative as:

Now pick safe upper and lower bounds for your $\delta$, to use for bisecting:

delta:=0; delta_b:=0.32; N:=100; eps:=0.01;

And then use bisection on your range $[0,\delta_b]$, to obtain some approximations. Whenever the calculated approximation for $\delta$ exceeds your test (meaning : $u_n'(x)\ge 1+\epsilon$), you replace $\delta_b$ with this $\delta$, and continue with bisection on the new interval $[0,\delta_b']$. For example:

After the loop runs, ask for $\delta_b$:

delta_b;

With $N=1000$, I get:

delta_b; 0.3132776394

which is correct to 9 decimals. Running this with higher decimal precision (Maple uses 10 by default), will bring you of course in more digits accuracy.

---

Addendum#1:

Adding a little code to watch the dynamics of this sequence on the complex plane. First, modify $u_n$ to accept a complex argument:

Some code for constructing the Julia set of the corresponding exponential sequence:

W:=LambertW;

eps:=0.01;

Now we can watch the dynamics of the $u_n(z)$ sequence dynamically on the complex plane:

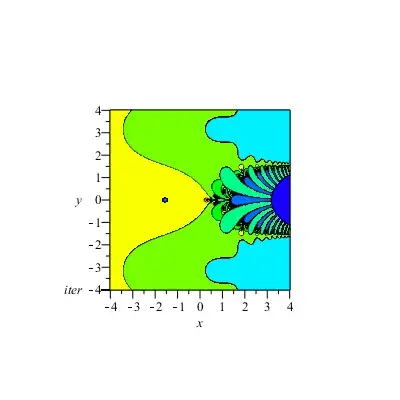
The above gives:

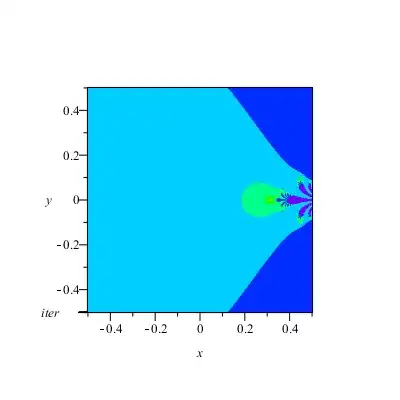
And magnified near the origin (without escape contours):

So your $\delta_{[0.313277...,0]}$ is the tip of the Julia Cantor Bouquet produced by $u_n(z)$. There are infinately many other such $\delta_{z}$, on the plane: All the yellow bouquet tip points on the sub-bouquets of the main bouquets, on the sub-sub-bouquets and so on.

This Julia set is similar to the Julia set for the plain exponential iteration of $E_{\lambda}(z)=\lambda e^z$, with $\lambda<1/e$ (more here). The only difference is that your sequence iterates $E_{\lambda_n}(z)$ for $\lambda_n=1/n$. All iterates except the first 2, have $\lambda_n<1/e$, so the Julia set is a plain Cantor Bouquet plus a Fatou domain (all colored domains in lighter shades than purple). Iterating any point from these Fatou domains will eventually cause the sequence to converge to the only convergent, the point: $z_0\sim 0.02041244406...$.

Iterating a point picked from the bouquet itself - except an endpoint, will shoot the orbit to complex infinity. (That's why if you pick $x>0.313277...$, the sequence diverges: Because such a point lies on the main "hair" of the Cantor Bouquet.) Hence, your $\delta$ is the tip of the main Bouquet of the Julia set.

(If your program allows for complex arguments, you can test other such values, for example: $\delta_{[3.1234256..,-1]}$, etc.).

The colors indicate speed of convergence: Blues are fastest, followed by greens and finally yellows and reds slower. But everything outside the bouquet eventually goes to $z_0$, including the tips of the bouquet.

To generalize finding more such $\delta_z$, just iterate for complex solutions to $|u_n'(z)|=1$.

Answer 3

I am proving something about $\delta$, namely the divergence of the sequence starting from $\delta$, see the Result below. This was the question in the OP. Some numerical aid is added to show how the "sequence works", and to give some support to the arguments involved.

---

To have a precise notation, i will fix an $x>0$ and define for it recursively $u_0(x)=x$ and $u_n(x)=\frac 1 n\exp u_{n-1}(x)$ for an integer $n>0$. A first useful observation is the following one.

Lemma 1: Assume $u_n(x)\ge u_{n+1}(x)$. Then $$ u_n(x) \ge u_{n+1}(x) > u_{n+2}(x) > u_{n+3}(x) > u_{n+4}(x) > \dots $$ so $(u_N(x))_{N\ge n}$ is a strictly decreasing sequence of positive numbers, and thus a convergent sequence.

Proof: Let $s$ be $u_n(x)$. We know $s\ge \frac{e^s}{n+1}$. Then $$ \begin{aligned} u_{n+1}(x)=\frac{\exp s}{n+1} &> \frac{\exp\frac{e^s}{n+1}}{n+2}=u_{n+2}(x) &&\text{ is equivalent to}\\ \underbrace{ \frac {n+2}{n+1}}_{>1} &>\exp\underbrace{\left(\frac{e^s}{n+1}-s\right)}_{\le 0}\ , \end{aligned} $$ and the last relation is clear, since the $1$ separates the two expressions. Inductively, all other comparison signs between two consecutive terms remain $>$ and we obtain convergence.

---

Lemma 2: Fix $x>0$. Assume that the sequence $(u_n(x))_{n\ge 0}$ is monotone and increasing. Then it is unbounded.

Proof: Assume there is a constant $M$ (upper bound) such that $$ x=u_0(x)\le u_1(x)\le u_2(x)\le \dots \le M\ . $$ We adjust $M$ to be minimal with this property. For any $\epsilon>0$ we have infinitely many terms of the sequence in the interval $(M-\epsilon,\epsilon]$, all terms with index $n\ge n_0$ for some suitable $n_0=n_0(\epsilon)$, so that for any $n\ge n_0$ $$ M-\epsilon\le u_{n+1}(x)=\frac 1{n+1}\exp u_n(x)\le\frac 1{n+1}\exp M\ . $$ We let $n$ not go to infinity, obtaining a contradiction for $\epsilon=M/2$ from $M/2\le\frac 1{n+1}e^M$.

$\square$

---

Consider now the set $C$ of all $x$ so that $(u_n(x))$ is convergent. This set is an interval (is convex) since from $x\in C$ we obtain $y\in C$ for all positive $y\le x$. The OP denotes by $\delta$ the number $\delta=\sup C$. It is clear that for any $x>\delta$ we have $u_n(x)\nearrow\infty$.

The question in the OP asks explicitly for the nature of the series $x_n(\delta)$.

---

To investigate what happens "in $\delta$" we use the analysis in the part of $(0,\infty)$ that "we better know", which is the convergence domain $C$. It is maybe useful to introduce some numerical discussion, just to show how the "sequence works". We have $u_0(x)=x<x+1\le e^x=u_1(x)$. Assume now $x\in C$. By Lemma 2, the sequence $u_n(x)$ is not strictly increasing. So at some point it decreases. By Lemma 1 the sequence keeps the decreasing character after this point. So it makes sense to speak of the first point $N=N(x)$ where the sequence becomes a decreasing sequence, i.e. $$ u_0(x)<u_1(x)\le \dots\le u_{N-1}(x)\le \boxed{u_N(x)}>n_{N+1}(x)>u_{N+2}(x)>\dots\ . $$ For instance, for $x=0.313$ we have numerically

? {a=0.313;
   for(n=1, 20, aa=exp(a)/n;
       print1("u_", n, " = ", aa);
       if(a < aa, print("  BIGGER"), print("  smaller"));
       a = aa;)}
u_1 = 1.3675215310276052580156244485205873317  BIGGER
u_2 = 1.9628045639746968825527107313466628204  BIGGER
u_3 = 2.3730885094556717601582056878568478087  BIGGER
u_4 = 2.6826205886314247378465092031314923147  BIGGER
u_5 = 2.9246729901579251786653681066911054540  BIGGER
u_6 = 3.1046889118003658683779460180009380929  BIGGER
u_7 = 3.1860399885563785616430186856926073497  BIGGER
u_8 = 3.0240543978924587401724975895522475423  smaller
u_9 = 2.2860600201376727553284809922492204883  smaller
u_10 = 0.98361071715125928138755201449968838114  smaller
u_11 = 0.24309947539391373305256660173652401198  smaller
u_12 = 0.10626628903174564052002058114668744999  smaller
u_13 = 0.085547537069273768253858963967751083770  smaller
u_14 = 0.077808095919794710713595034674642307547  smaller
u_15 = 0.072061013781783719666740623208530533727  smaller
u_16 = 0.067170057178175596313653825639495171561  smaller
u_17 = 0.062910431471108603831434935127199016802  smaller
u_18 = 0.059162858367558800252445283831682027556  smaller
u_19 = 0.055839368996440348276611168751081353904  smaller
u_20 = 0.052871390720140815464124735441909317362  smaller

So $N(0.313)=7$, and the same code starting with a=0.3132 gives $N(0.3132)=8$:

u_1 = 1.3677950626860648528324517882175013160  BIGGER
u_2 = 1.9633415265971033194641148584052431230  BIGGER
u_3 = 2.3743631114611039626890639195230221387  BIGGER
u_4 = 2.6860420422461167457807641681804189877  BIGGER
u_5 = 2.9346967612874001121755801606161241533  BIGGER
u_6 = 3.1359660986784763145732917033109680528  BIGGER
u_7 = 3.2872651234829478358588813251548230858  BIGGER
u_8 = 3.3461940041560052698109444803350566130  BIGGER
u_9 = 3.1549398373315806806605530408402914704  smaller
u_10 = 2.3451626136580891634913767329764798075  smaller
u_11 = 0.94863358710409358130678000785727277093  smaller
u_12 = 0.21518157708850363361007658962635940641  smaller
u_13 = 0.095391311378459099032647088551719786951  smaller
u_14 = 0.078577803453709167722261045262294803777  smaller
u_15 = 0.072116501038733476706519017436400138429  smaller
u_16 = 0.067173784363802268615874765719256293850  smaller
u_17 = 0.062910665950401524353995891488337534298  smaller
u_18 = 0.059162872240025623837696802595148633706  smaller
u_19 = 0.055839369771070147502677863568128329238  smaller
u_20 = 0.052871390761096570258333115181710141051  smaller

We need a lemma cementing this observation.

---

Lemma 3: If $x\le x'$ then $N(x)\le N(x')$.

In other words, if we define for $N\ge 1$ the set $C_N$ to be the set of all $x$ so that $N(x)=N$, then $C_1 <C_2<C_3<C_4<\dots$ .

Proof:

Starting from $x=0$ we obtain $u_1(0)=1$, $u_2(0)\approx 1.359\dots$, $u_3(0)\approx 1.29$, so $0\in C_2$.

• The set $C_1$ is thus empty. (It is the set of all $x$ so that $$ x=u_0(x)< \boxed{u_1(x)}\ge u_2(x)\ . $$ The inequality $\le $ is valid on the interval with $u_1(x)\ge \frac 12\exp u_1(x)$. This happens, if it happens, for $x$ on an interval $C_1=(0,c_1]$, so that for $y=u_1(x)=e^x>0$ we have $y\ge \frac 12\exp y$. There is no such $y$, so the set $C_1$ is empty.)

• The set $C_2$ is the set of all $x$ so that $$ x=u_0(x) < u_1(x)< \boxed{u_2(x)}\ge u_3(x)\ . $$ The inequality $\le $ is valid on the interval with $u_2(x)\ge \frac 13\exp u_2(x)$. This happens, and it happens, for $x$ on an interval $C_2=(0,c_2]$, so that for $y=u_2(x)>0$ we have $y\ge \frac 13\exp y$. The maximal value is $y=u_2(c_2)$, and this is the solution $w_2>1$ of the transcendental equation $$ y=\frac 13 e^y \ . $$ We have solutions, and $w_2\approx 1.5121345516\dots$, so $c_2=u_2^{-1}(w_2)\approx 0.101355\dots$ . For all other values $x>c_2$ we have $u_0(x) < u_1(x)< u_2(x) <u_3(x)$.

• The set $C_3$ is the set of all $x>0$, $x\not\in C_2$, so $x>c_2$, so that $$ x=u_0(x) < u_1(x)< u_2(x) < \boxed{u_3(x)}\ge u_4(x)\ . $$ The inequality $\le $ is valid on the interval with $u_3(x)\ge \frac 14\exp u_3(x)$. This happens, if it happens, for $x$ on an interval $C_3=(c_2,c_3]$, so that for $y=u_3(x)> u_3(c_2)=u_2(c_2)$ we have $y\ge \frac 14\exp y$. The maximal value is $y=u_3(c_3)$, and this is the solution $w_3>1$ of the transcendental equation $$ y=\frac 14 e^y \ . $$ We have solutions, and $w_3\approx 2.15329236411\dots$, so $c_3=u_3^{-1}(w_3)\approx 0.27515550\dots$ . For all other values $x>c_3$ we have $u_0(x) < u_1(x)< u_2(x) <u_3(x) < u_4(x)$.

• And the procedure goes on. For a general $n$ we define $w_n>1$ to be the solution of the equation $$ y = \frac 1{n+1}e^y\ , $$ then we set $c_n=u_n^{-1}(w_n)$. Then $C_n=(c_{n-1},c_n]$ defined to be the set where we have $$ x=u_0(x) < u_1(x)< u_2(x) < \dots <\boxed{u_n(x)}\ge u_{n+1}(x)\ . $$

For all other values (not considered yet, i.e.) $x>c_n$ we have $u_0(x) < u_1(x)< u_2(x) <\dots <u_n(x) < u_{n+1}(x)$.

(At the last place we have a strict inequality making the last term strictly bigger than the previous one(s).)

• The only thing we have to show is the following one: For all $n>2$ we have the inequality marked with an exclamation mark: $$ c_n\overset !< c_{n+1}\ . $$ Equivalently, after applying $u_{n+1}$ first, we have successively: $$ \begin{aligned} c_n& \overset !< c_{n+1}\ , \\ u_{n+1}(c_n)& \overset !< u_{n+1}(c_{n+1})\ , \\ \underbrace{\frac 1{n+1}(\exp u_n(c_n)}_{=w_n}& \overset !< w_{n+1}\ , \\ w_n&\overset !< w_{n+1}\ .\\ n+1&\overset !< n+2 \end{aligned} $$ The last step is clear because the function $\frac 1ye^y$ is strictly monotone on the interval of interest $[3,\infty)$.

---

Result: The sequence $(c_n)$ is bounded. (For instance $c_n\le 1$.)

Let $\delta$ be its limit, $\delta=\lim c_n=\sup c_n$.

Then $(u_n(\delta))$ diverges.

Proof: Because $\delta>c_n$ for all $n$ we have $$u_0(\delta)<u_1(\delta)<u_2(\delta)<u_3(\delta)<\dots<u_n(\delta)<\dots\ . $$ By Lemma 2 we get an unbounded sequence.

$\square$

---

Numeric evidence:

I will user again pari/gp . Then the first values for $w_=w(n)n$ are:

? \p 60
   realprecision = 77 significant digits (60 digits displayed)
? for(n=2, 10, wn = solve(y=1, 10, exp(y)-(n+1)*y); print("w(", n, ") ~ ", wn);)
w(2) ~ 1.51213455165784247389673967807203870460365038513535945425929
w(3) ~ 2.15329236411034964916909915009298137553620648531947769588451
w(4) ~ 2.54264135777352642429380615666184829016147490752943176711693
w(5) ~ 2.83314789204934214261167464234313256401468427714756512323373
w(6) ~ 3.06642134506926941241072450697636490912388231023308379327649
w(7) ~ 3.26168568457648877690566236430873973172114539334780952204022
w(8) ~ 3.42969628915899382743138865331419512387682622454177359601026
w(9) ~ 3.57715206395729721840939196351199488040179625779307592368353
w(10) ~ 3.70853115627103351156855721025086632923025483851609038044510

(Pari/GP has only the pricipal brance of the lambertw function.) In sage we can use also other branches of this function. We rewrite the transcendental equation $$ y =\frac 1{n+1}e^y $$ in the form $$ (-y)e^{-y}=-\frac 1{n+1} \ , $$ which gives $w_n=W_{-1}(-1/(n+1)$ . Sage gives then the values:

for n in [2..10
     wn = -lambert_w(-1, -1/(n+1)).n(digits=60
     print(f"w({n}) ~ {wn}")
w(2) ~ 1.51213455165784247389673967807203870460365038513535945425929
w(3) ~ 2.15329236411034964916909915009298137553620648531947769588451
w(4) ~ 2.54264135777352642429380615666184829016147490752943176711693
w(5) ~ 2.83314789204934214261167464234313256401468427714756512323373
w(6) ~ 3.06642134506926941241072450697636490912388231023308379327649
w(7) ~ 3.26168568457648877690566236430873973172114539334780952204022
w(8) ~ 3.42969628915899382743138865331419512387682622454177359601026
w(9) ~ 3.57715206395729721840939196351199488040179625779307592368353
w(10) ~ 3.70853115627103351156855721025086632923025483851609038044510

Since i rather trust the precision in pari/gp, i will compute some $c_n$-values in pari/gp:

? {c(n) = wn = solve(y=1, n, exp(y)-(n+1)*y);
          a = wn;
          for( kk=1, n, k=(n+1)-kk; a = log(k*a) );
          a; }
? \p 50
   realprecision = 57 significant digits (50 digits displayed)
? for(n=2, 60, print("c(", n, ") &\sim", c(n), "\dots\\"));

The results are suited to a copy+paste action into an aligned block:

$$ \begin{aligned} c(2) &\sim0.10135500348877619648835046893307802134647843854859\dots\\ c(3) &\sim0.27515550224356722642700029292669340425790411988586\dots\\ c(4) &\sim0.30440354255780715384928950088935566512074662284688\dots\\ c(5) &\sim0.31111934109691133707464026297298705606522340312816\dots\\ c(6) &\sim0.31275095307818668153209240588697305474570060282017\dots\\ c(7) &\sim0.31315034197961514476112541848049188150250410074878\dots\\ c(8) &\sim0.31324730472844731441045222549671358612256305068358\dots\\ c(9) &\sim0.31327052241203616368893190165080929026601998047499\dots\\ c(10) &\sim0.31327599571763732522624466142920222534452300093615\dots\\ c(11) &\sim0.31327726562968841826282081670459211837048707198094\dots\\ c(12) &\sim0.31327755572894389701305007274609305684358656586721\dots\\ c(13) &\sim0.31327762101787184872963296682754422073736624513741\dots\\ c(14) &\sim0.31327763550439768085446246483894501667765926971232\dots\\ c(15) &\sim0.31327763867571006703555595324736062516361585176649\dots\\ c(16) &\sim0.31327763936115504573935501667287678447210707448810\dots\\ c(17) &\sim0.31327763950752672055982251214461261883812504160744\dots\\ c(18) &\sim0.31327763953842719229730321612969220129090235414359\dots\\ c(19) &\sim0.31327763954488001621055885793746377925086787133883\dots\\ c(20) &\sim0.31327763954621367609922944945670217886704627412091\dots\\ c(21) &\sim0.31327763954648661595904784671869579247553003455047\dots\\ c(22) &\sim0.31327763954654195287253067161058269140404032890270\dots\\ c(23) &\sim0.31327763954655307206776515886125074035389761846850\dots\\ c(24) &\sim0.31327763954655528726715108843199348672484120918294\dots\\ c(25) &\sim0.31327763954655572498212771123141999427090570670146\dots\\ c(26) &\sim0.31327763954655581079567023002593270768368799867357\dots\\ c(27) &\sim0.31327763954655582749282669405759711979793525735967\dots\\ c(28) &\sim0.31327763954655583071818919874759817293462259261239\dots\\ c(29) &\sim0.31327763954655583133689251460813922039357123411747\dots\\ c(30) &\sim0.31327763954655583145477928547388335070258877443942\dots\\ c(31) &\sim0.31327763954655583147709599602419284510657691971650\dots\\ c(32) &\sim0.31327763954655583148129431164142194407675946396456\dots\\ c(33) &\sim0.31327763954655583148207935057505826128744893134496\dots\\ c(34) &\sim0.31327763954655583148222528727352500245553858308174\dots\\ c(35) &\sim0.31327763954655583148225226318204998596936649150874\dots\\ c(36) &\sim0.31327763954655583148225722227611323237580761358174\dots\\ c(37) &\sim0.31327763954655583148225812908456600452851730734627\dots\\ c(38) &\sim0.31327763954655583148225829404662758602316288107775\dots\\ c(39) &\sim0.31327763954655583148225832390544808433831911964086\dots\\ c(40) &\sim0.31327763954655583148225832928371927863800658191742\dots\\ c(41) &\sim0.31327763954655583148225833024788691497864879533556\dots\\ c(42) &\sim0.31327763954655583148225833041993809498564822525567\dots\\ c(43) &\sim0.31327763954655583148225833045050213708406158795592\dots\\ c(44) &\sim0.31327763954655583148225833045590796516903409149109\dots\\ c(45) &\sim0.31327763954655583148225833045686001554718024594137\dots\\ c(46) &\sim0.31327763954655583148225833045702698985929467652069\dots\\ c(47) &\sim0.31327763954655583148225833045705615574487227907134\dots\\ c(48) &\sim0.31327763954655583148225833045706123006980155619276\dots\\ c(49) &\sim0.31327763954655583148225833045706210949522978129814\dots\\ c(50) &\sim0.31327763954655583148225833045706226133158177531860\dots\\ c(51) &\sim0.31327763954655583148225833045706228744990391540019\dots\\ c(52) &\sim0.31327763954655583148225833045706229192644777682540\dots\\ c(53) &\sim0.31327763954655583148225833045706229269099154514550\dots\\ c(54) &\sim0.31327763954655583148225833045706229282111523143202\dots\\ c(55) &\sim0.31327763954655583148225833045706229284318695085698\dots\\ c(56) &\sim0.31327763954655583148225833045706229284691835169076\dots\\ c(57) &\sim0.31327763954655583148225833045706229284754712279749\dots\\ c(58) &\sim0.31327763954655583148225833045706229284765273792594\dots\\ c(59) &\sim0.31327763954655583148225833045706229284767042269982\dots\\ c(60) &\sim0.31327763954655583148225833045706229284767337485177\dots\\ \end{aligned} $$