Finding a counterexample

Question

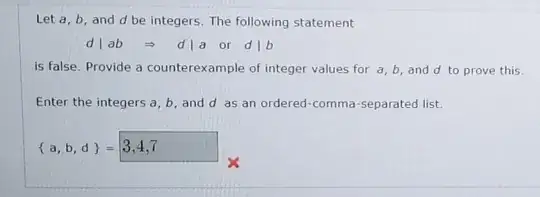
Why is this wrong? Doesn't $a | b$ mean $a$ divides $b$ so $b = a(x)$?

So then if $a=3, b=4, d=7$ then

$d | ab$ will mean $12 = 7(12/7)$, $d | a$ will mean $3 = 7(3/7)$, $d | b$ will mean $4 = 7(4/7)$

so $d | ab$ is not equal to $d | a$ or $d | b$

doesn't that mean this is a counterexample?

I must be not understanding it correctly.

Can someone please explain?

$d|ab$ means $ab =dn$ for some integer $n$. – Kavi Rama Murthy Sep 17 '20 at 08:32 — Kavi Rama Murthy, Sep 17 '20 at 08:32

score 2 · Answer 1 · answered Sep 17 '20 at 08:33

2

A valid counterexample is a pair $(a,b,d)$ for which $d \mid ab$ but $d$ divides neither $a$ nor $b$. You took $a = 3$, $b = 4$, and $d = 7$. Observe that $d$ does not divide $ab = 12$, so the implication in question is vacuously true.

answered Sep 17 '20 at 08:33

MathGuySam

67
5

Would d = 6, a = 2. b = 27 be a counterexample? – user30200 Sep 17 '20 at 08:58
Does 'dividing' include the answer being a fraction? – user30200 Sep 17 '20 at 09:00

user926356 · Accepted Answer · 2020-09-17T09:21:14.453

0

$a|b$ means that there exists a number $z\in\mathbb{Z}$ such that $az=b$. For example, $3|18$ is true because there is an interger $z$ ($6$ in this case) such that $3z=18$. $4|5$ is false because there is no interger $z$ such that $4z=5$. So we say that $4\nmid 5$. $7|-28$ is true because $z=-4$ (which is clearly an interger) satisfies $7$x$z=-28$

As a counter example you can consider $a=2, b=6,$ and $d=4$. So we have that $ab=12$ and $4|12$ (since $4$x$3=12$). But $4\nmid 2$ and $4\nmid 6$

edited Sep 17 '20 at 09:21

answered Sep 17 '20 at 08:57

user926356

1,250

Ohh so when you divide two numbers and the answer is a fraction then it means they don't divide? – user30200 Sep 17 '20 at 09:01
@user30200, Yes. Another -but equivalent- way to interpret $a|b$ is that $b$ is a multiple of $a$. If $b$ is not a multiple of $a$, then $a\nmid b$. In other words, there is no number $z\in\mathbb{Z}$ that satisfies $az=b$. – user926356 Sep 17 '20 at 09:12
@user30200, It's also important to note that every integer can be expressed as a fraction, but not every fraction represents an integer. For example, $8/4$ is an integer, and so are $21/3$ and $117/1$. But $1/15$ is not, and neither are $5/3$ and $23/15$. So if $b$ divided by $a$ equals a fraction that represents an integer, then $a|b$. But, if such fraction is not an integer, then $a\nmid b$. Did this help? – user926356 Sep 17 '20 at 09:38

Finding a counterexample

2 Answers2