Legendre symbol for (2/p)

Asked Sep 14 '20 at 16:50

Active Sep 14 '20 at 16:50

Viewed 415 times

I'm reading a proof that $$ (2/p) = (-1)^{\frac{p^2 -1}8} $$ for odd primes $p$. I follow the proof upto and including this line:

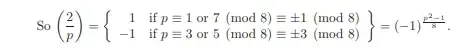
Which follows from the fact $$p \equiv \pm 1 \pmod 8 \implies \frac{p^2 -1}8 \equiv 0 \pmod 2 \tag{1} $$ and similarly $$p \equiv \pm 3 \pmod 8 \implies \frac{p^2 -1}8 \equiv 1 \pmod 2 \tag{2}. $$

However to convince myself of these last facts I had to write $p = 8k +1$ and go from there etc. Is there an easy way to (1) and (2), or at least a way to show it without leaving modular arithmetic?

I'm sure I'm missing something obvious, but several of the proofs in this course involve similar deductions and I'd rather know the simpler route, thanks!

asked Sep 14 '20 at 16:50

Red Grassrex

1

A shortcut is to show $p^2\equiv 1\mod 16$ , if $p\equiv \pm1\mod 16$ or $p\equiv \pm9\mod 16$. Try to find an analogue proof for the second case. – Peter Sep 14 '20 at 17:26
1

If $8|p\pm1$, then $16|(p\pm1)(p\mp1)$, but if $16\nmid (p-1)(p+1)$, then $8\nmid p\pm1$ – J. W. Tanner Sep 14 '20 at 17:28
@Peter: I think you'd be interested in this question – J. W. Tanner Sep 14 '20 at 17:31
@J.W.Tanner In factordb, the smallest unknown case is $n=2^{14}$, but if I understood the answers right, the exponents upto at least $2^{15}$ have also been checked. Is that right ? – Peter Sep 14 '20 at 17:41
@Peter: Thanks thats what i was looking for, I see how it would work in the second case too. Am i right in saying the general fact we're using is that $a \equiv b \pmod m \implies a \equiv b, b + m, b + 2m, ... $ or $b+(n-1)m \bmod nm$? – Red Grassrex Sep 14 '20 at 17:47
@Peter: I think so – J. W. Tanner Sep 14 '20 at 18:25
@RedGrassrex: cf. mod distributive law – J. W. Tanner Sep 15 '20 at 14:56

Legendre symbol for (2/p)

0 Answers0