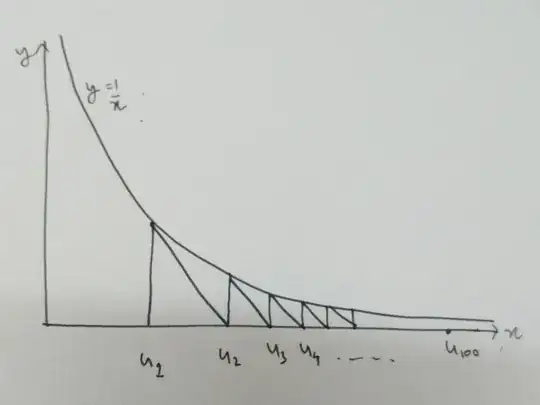
$u_1 = 1$
$u_{n+1} = u_n + 1/u_n$ for $n > 1$.
Find $\lfloor 50u_{100}\rfloor$, where $\lfloor x\rfloor$ represents the greatest integer less than or equal to $x$.
Kindly give any clues/ideas on how to approach this problem. I know the answer via a simple program I wrote. (Answer = $710$) How do I solve this analytically?
So far I've been able to see a pattern on $y = 1/x$ graph: start on $(1, 1)$ go down diagonally along $x+y=0$, hit x-axis and go straight up, hit the curve and keep repeating these right triangles. Not sure if this helps but I'm not able to proceed any further.